ASPECTOS REPRODUCTIVOS Y APROXIMACIÓN A UN MODELO DE CRECIMIENTO PARA UNA POBLACIÓN DE Macrobrachium acanthurus (WIEGMANN, 1836) EN EL RÍO PALIZADA, CAMPECHE, MEXICO

Trabajo recibido el 24 de junio de 1992 y aceptado para su publicación el 17 de noviembre de 1993.

RESUMEN

INTRODUCCIÓN

En el período de los años sesenta y setenta el interés por los langostinos del géneroMacrobrachium creció considerablemente en todo el mundo (Ling, 1962, 1969; Ardill y Thompson, 1975; Dugan et al., 1975; Kloke y Potaros, 1975), debido a la potencialidad que algunas especies representaron para el cultivo.

En México, algunos años antes, surgió el interés hacia este grupo con el trabajo de Mercado (1959); desde entonces, numerosas investigaciones han sido publicadas en el país sobre diversos aspectos de Macrobrachium (Rodríguez de la Cruz, 1968; Arana, 1974; Chávez Alarcón y Chávez, 1976; CabreraCano, 1980; Guzmán et al., 1982; Granados Ber- 1984; y Román Contreras, 1979 y 1991, entre otros).

Como puntos relevantes de las poblaciones naturales o en cultivo se consideran la fecundidad y el crecimiento de los individuos; la primera es un aspecto ecológicamente importante de la población y el estudio de vida de cualquier especie (Corey y Reid, 1991) porque permite mantener los niveles de la po Blación; el segundo, porque el objetivo primordial en las prácticas de acuacultura es la producción de organismos de tallas óptimas en el tiempo más corto y al menor costo posible con miras a su consumo.

Entre las especies deMacrobrachium existe amplia información paraM. rosenbergii, especie asiática que es considerada el prototipo para propósitos de acuacultura (Hanson y Goodwin, 1977; New, 1982).

Sin embargo, la información sobre este aspecto para las especies americanas es notablemente escasa, por lo que los objetivos del presente trabajo son:

a) Generar información sobre aspectos reproductivos y sexuales de M. acanthurus en el área de estudio;

b) Estimar su ritmo de crecimiento en condiciones naturales; y

c) Coadyuvar a la integración de un marco de referencia para la evaluación, protección y manejo del recurso.

El área se localiza en la porción suroccident laLagunadeTérminos,denominada "Palizada del Este-Boca Chica"; se ubcoordenadas 18º 29' 44" y los 18º 29' 04" de latitud septentrional y los 91º 44' 36 y los 91º 51 31" de longitud occidental (Vera-Herrera et al.,1988).

Las estaciones de colecta se ubicaron en el borde del Río Palizada, en la porción final del sistema fluvio-lagunar, aproximadamente un kilómetro antes de su desembocadura al interior de la Laguna de Términos. Se caracterizaron predominantemente por la presencia de vegetación tipo tular y carrizal, de acuerdo con la clasificación de Rzedowsky (1978).

Las temperaturas anuales en esta área son superiores a 26ºC, y las precipitaciones oscilan entre 1,100 y 2,000 mm. El clima es cálido, subhúmedo e isotermal, con lluvias en verano (Vera-Herrera et al.,1988).

Se realizaron muestreos bimensuales en el sistema mencionado; para las colectas de utilizaron redes de cuchara y patín, o se hicieron manualmente cuando fue posible. Los organismos fueron fijados en alcohol al 70% para su transporte y conservación.

En el laboratorio, éstos fueron medidos con vernier en su longitud total, tomando como base la punta del rostro hasta la punta del telson, así como la longitud del cefalotórax. El peso fue registrado mediante el uso de una balanza de triple brazo con 0.1 gramo de precisión para los organismos adultos y con una balanza analítica en el caso de los juveniles.

De los adultos se contó el número de hembras y machos para conocer la proporción de sexos en la población.

De las hembras ovadas fue separada la masa ovígera con pinzas y agujas de disección; de ésta se eliminó el exceso de líquido y se tomó una submuestra de huevecillos para su conteo directo; del resultado se hizo una extrapolación para conocer el total de huevecillos por hembra.

Los registros biométricos de los organismos se analizaron por el método descrito por Gulland (197 1) y Pauly (1983) para elaborar modelos de crecimiento poblacional. El primer paso fue obtener la relación entre la longitud total y el peso total de los organismos en forma global (machos y hembras juntos) mediante la expresión potencial:

P = a L

o en su forma logarítmica:

log P = log a + b log L

donde:

P =peso calculado en gramos

L =longitud total registrada en milímetros

a y b = constantes obtenidas a partir de una regresión entrePyL, cona = ordenada al origen y

b = pendiente, donde el valor de este parámetro permite conocer el tipo de crecimiento de la población y define la proporción con que aumenta el peso con respecto a la longitud.

Para reforzar el análisis del tipo de crecimiento de la especie se efectuó un estudio de correlación entre la longitud del cefalotórax y la longitud total.

Posteriormente se gráfico la longitud total contra la frecuencia, para obtener las medias modales representativas del tamaño de los organismos que definieron las diferentes clases de edad, según el método de Petersen (1892) descrito por Schnute y Fournier (1980) y complementado por el método de Bhattachary a (1967). Con los valores resultantes se elaboró un gráfico de Ford-Walford, que representa una regresión de valores de longitudes consecutivas, a través del cual se pudo inferir la longitud máxima que alcanzan los individuos en la población. La expresión matemática que fundamenta este proceso es la ecuación empírica desarrollada en forma independiente por Ford y Walford (Ricker, 1975), donde: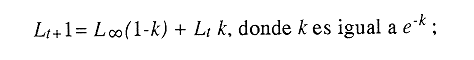

o en la forma sugerida por Gulland (1971), donde: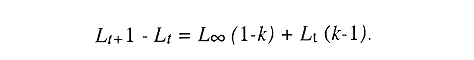

La pendiente resultante de la línea de regresión en la gráfica representa el valor de K = e^-k , donde 'K' es una constante de crecimiento. Esta línea de regresión al interceptarse con otra línea de pendiente igual a uno dio el valor de L∞, que representa el valor máximo de longitud alcanzable en la población.

Para el cálculo de crecimiento se utilizó la ecuación de von Bertalanffy (1938), que ha sido ampliamente utilizada por Cruz (1968), Boschi (1969), Chávez (1973), Chávez y Rodríguez de la Cruz (1971), y Parrack (1979), para peneidos; y por Chá- y Chávez (1976), Guest (1979) y Bond y Buckup (1983), para langostinos. Esta ecuación se el expresa como: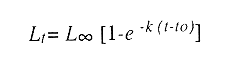

donde:

t_o= tiempo teórico en el que el organismo inicia su crecimiento

t =clase de edad a la que se desea estimar la longitud

L∞ =longitud teórica infinita

k =constante de crecimiento

L_t = longitud al tiempot.

Partiendo del supuesto de que los intervalos de tiempo son iguales, y para conocer el tiempo hipotético en el cual el organismo inició su crecimiento, se utilizó la siguiente ecuación que corresponde a un ajuste del modelo de von Bertalanffy: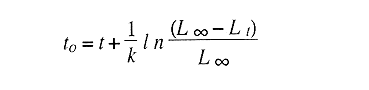

Al utilizar la relación de longitud y peso de los individuos se obtuvo el valor del peso máximo (Poo), el cual fue sustituido en la ecuación de crecimiento que queda de la siguiente forma: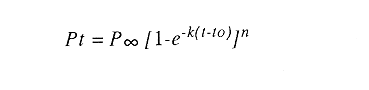

donde:

Pt= peso al tiempo't' y

n = valor de la pendiente de la relación Peso-Longitud.

El análisis estadístico se realizó según los métodos descritos por Sokal y Rholf (1969), Daniel (1980) y Márquez (1988), e incluyó regresiones, co- y pruebas de hipótesis, así como estadísticos básicos que incluyeron medias, modas y polígonos de frecuencia.

En el área delimitada para el presente estudio se colectaron 1,083 individuos entre juveniles y adultos deM. acanthurus,de los cuales se tomó una muestra de 174 organismos mayores de 30 mm de longitud total y se calculó la proporción de un macho por cada 1.6 hembras.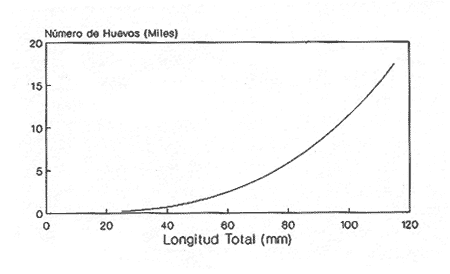

Figura 1. Relación entre la fecundidad y la longitud de M. acanthurus.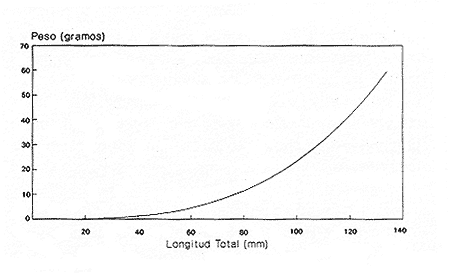

Figura 2. Relación entre la longitud y el peso de M. acanthurus.

Época reproductiva. Durante el período de marzo a noviembre se colectaron hembras ovigeras, siendo la máxima colecta durante mayo, mientras que en diciembre su presencia fue nula.

Sin embargo, organismos juveniles de M. acanthurus menores a 20 mm de longitud total se colectaron durante todas las sesiones, lo cual significa que las hembras desovan durante todo el año.

Madurez sexual. La talla mínima registrada de hembras sexualmente maduras fue de 35 mm de longitud total, que corresponde a una edad aproximada de seis meses.

Fecundidad El número mínimo de huevos registrados en hembras de M. acanthurus fue de 720, longitud total de 35 mm, y el máximo de 14,840 en una hembra con longitud total de 110 mm. El índice de fecundidad y su relación respecto al tamaño de los organismos fue potencial (Fig. 1); se observó que la ecuación que rige este comportamiento es: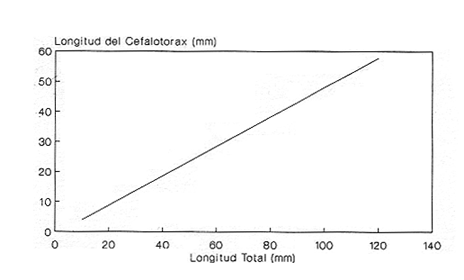

Figura 3. Relación entre longitud total y longiud del cefalotórax.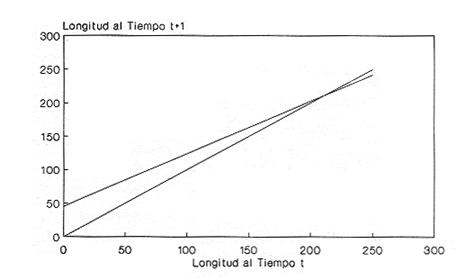

Figura 4. Gráfico de Ford-Walfórd.

F =0.0105L^3.0181

donde:

L = longitud total

F =fecundidad (numero de huevecillos)

0.0105 = intercepto y

3.0181 = valor de la pendiente.

El peso de la masa ovigera representó entre 14.5 y 19.9% del peso corporal de los individuos observados.

Crecimiento: Relación longitud-peso.El 17% de la muestra poblacional correspondió a tallas mayores o iguales a 30 mm. La talla máxima fue de 176 mm de LT y el peso de 50 g; los promedios fueron 49 mm y 6.57 g para longitud y peso, respectivamente. A través de una prueba hipótesis, y mediante al estadístico "t" de Student adecuado para un modelo bivariado normal, se verificó la dependencia que existe entre las variables longitud y peso total de los organismos; con base en esta prueba, la hipótesis nula de independencia de variables fue rechazada a nivel de significancia de 5%.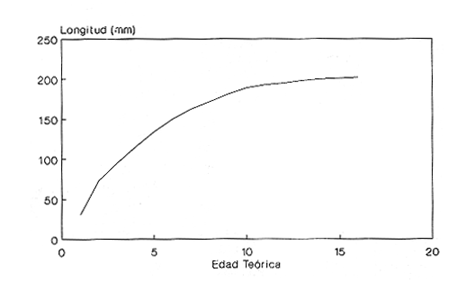

Figura 5. Curva de crecimiento.

Con el manejo de los datos de longitud total y el peso de 547 individuos, que incluyó la totalidad de los organismos de talla mayor a 30 mm, se determinó la relación entre estos parámetros, definiéndose una relación de tipo potencial (Fig. 2) representada por la expresión: P∞ = 4.15 x 10^-6+L^3.185; o en su forma logarítmica:log P= log 4.15 x 10^-6 + 3.185(log L),donde:

P = peso del organismo

L = longitud total

4.15 x 10^-6 = intercepto

3.185 = pendiente.

Relación longitud total-longitud del cefalotórax.Al relacionar la longitud de los especímenes con la del cefalotórax se presentó una alta correlación de tipo lineal; este comportamiento es representado en la figura 3 y a través de la expresión:

LC = 0.4897 (LT) + 0.998

donde:

LC =longitud cefalotorácica

LT =longitud total

0.998 = ordenada al origen

0.4897 =pendiente.

Clases de edades y ecuación del crecimiento.De acuerdo con los métodos de Petersen y Bhattacharya, se determinaron las clases de edad para todas las muestras de langostinos y se gráfico la frecuencia de los intervalos de talla, de donde resultó una distribución multimodal en la que las longitudes de los langostinos juveniles estuvieron mejor representadas.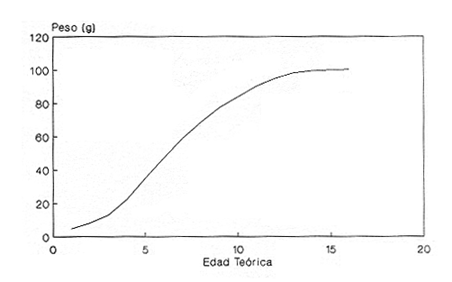

Figura 6. Curva de crecimiento en peso.

Para la obtención del gráfico de Ford-Walford se utilizaron las medias modales más representativas, las cuales se consideraron para ilustrar las longitudes de la población en tiempos sucesivos (L_tyL_t+1), quedando definidos como: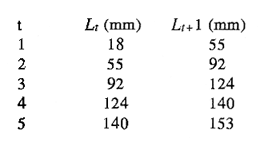

Al efectuar la regresión de los datos anteriores se obtuvo una línea recta cuyo comportamiento queda expresado como:

L_t+1 = 45. 345 + 0.7862 (L_t)

r =0.98

0.7862 =pendiente y

45. 345 =intersección

De esta regresión se calculó la longitud máxima hipotética alcanzada por los espéciménes de la población muestreada (L∞), al intersectar la línea resultante con una bisectriz de pendiente igual a 45º (Fig. 4).

Con el valor resultante de L∞ se procedió a calcular el valor del peso máximo que teóricamente alcanzan los organismos, y con base en la ecuación correspondiente a la relación peso-longitud de la figura 2, de donde se obtuvo que P∞ = 4.15 x 1O^-6L_∞^3.185.Sustituyendo estos valores:

P∞ =0.00000415 (212.06) ^3.185

P∞ = 106.6 g

Al sustituir los valores de L∞, P∞,tyk en las ecuaciones de longitud y peso del modelo von Bertalanffy se obtuvieron las expresiones matemáticas que describen el crecimiento de la especie:

a)Para la longitud: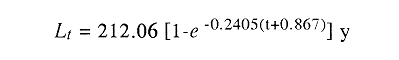

b) Para el peso: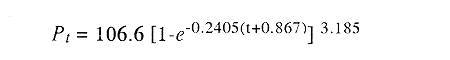

Utilizando estas ecuaciones se procedió a calcular los valores de longitud y peso para diferentes edades hipotéticas (Figs. 5 y 6).

La proporción sexual en las colectas analizadas no mostró ser paritaria, ya que se observó un macho por cada 1.6 hembras valor idéntico al calculado por Granados (1984) para la misma especie de langostinos en uno de los sitios de colecta de este autor. En el área del presente estudio la proporción sexual se debió a que la época de reproducción implica mayor permanencia de las hembras en las cercanías del estuario, donde las larvas encuentran gradientes de salinidad más adecuados para su desarrollo. Esta situación se ve favorecida porque los machos de la especie son objeto de captura selectiva por su mayor tamaño, hecho que se presenta en la mayoría de las especies de Macrobrachium dada su importancia comercial.

La reproducción M. acanthurus se lleva a cabo durante todo el año, puesto que se colectaron hembras grávidas en la mayoría de las sesiones de colecta e individuos jóvenes de 16 a 25 mm de longitud total en todas ellas.

Por otra parte, aunque la reproducción parece que es continua, no se presenta con la misma intensidad durante el año, pues aparentemente existen épocas con mayores índices de reproducción entre mayo y octubre; es decir, durante la temporada de lluvias.

Con relación a la fecundidad, se observa una correlación directa entre la longitud de las hembras y el número de huevecillos producidos por éstas (Fig. 1); y no obstante que la masa ovígera es distinta para cada talla, se conservan proporciones equivalentes al peso de los individuos.

Suponiendo la existencia de hembras ovigeras con tallas mayores a la máxima longitud registrada en este estudio (110 mm), la ecuación empírica de la relación longitud-fecundidad permite inferir que el número de huevos producidos por la especie es mayor al máximo registrado (14,840), ya que sugiere que un ejemplar de 135 mm de LT produciría aproximadamente 28,000 unidades. Los valores calculados por Román (1979) y Guzmán et al.,(1982) paraM. tenellum, especie muy similar a M. acanthurusen sus aspectos biológicos generales, son muy semejantes a los calculados por Cabrera-Cano (1980) y Granados-Berber (1984), quienes contabilizaron 6,00.0 y 5,500 huevecillos, respectivamente, en hembras deM. acanthurus con longitudes entre 70 y 75 mm de LT. Pero dichos valores son diferentes a los obtenidos en especies de mayor talla, comoM. americanum, especie para la que Mónaco (1975), Arana (1974) y Rodríguez de la Cruz (1968) calcularon 80,000; de 50,000 a 250,000; y de 200,000 a 500,000 huevecillos, respectivamente, dependiendo de la talla de las hembras, lo que hace que ésta sea una de las especies de mayor índice de fecundidad en el géneroMacrobrachium, seguida sólo deM. carcinus,cuyas hembras de 125 mm de LT llegan a tener hasta 35,580 huevecillos (Chávez-Alarcón y Chávez, 1976).

En contraste,Macrobrachium acanthurus borelii se encuentra entre las especies del género con menores índices de fecundidad; en ésta la cantidad de huevecillos que Bond y Buckup (1982) observaron fue de 53, con variaciones entre 15 y 118 huevecillos por hembra: mientras que en M. potiuna la cantidad osciló entre una y 57 unidades,ya que es de las especies que producen la menor cantidad de huevos entre los Palemó- (Bond y Buckup, 1982).

Macrobrachium acanthurus se sitúa entre las especies con índices de fecundidad media comparable sólo con M. tenellum y M. ohione, entre otras de tallas similares, pero lejos de los elevados valores de fecundidad dados a M. americanum y M. carcinus por un lado y los bajos valores que tienen M. borelii y M. potiunapor el otro lado.

De lo anterior se deduce que los valores de fecundidad en el géneroMacrobrachiumvarían de especie a especie dependiendo de sus respectivas tallas, pero en general se observa alta correlación entre la longitud de las hembras y la cantidad de huevecillos que producen, como ilustran los modelos de Chávez-Alarcón y Chávez (1976) para M. carcinus, de Hunte y Mahon (1983) para M. faustinum,y a M. acanthurus en el presente estudio. El análisis estadístico de la relación peso-longitud para la colecta global de langostinos muestra que la longitud y el peso total están estrechamente correlacionados, y que el segundo depende significativamente del primer elemento. El comportamiento de la relación entre estos factores es potencial, situación común que muestran los resultados de Boschi (1969), Chávez (1973) y Chávez y Rodríguez de la Cruz (1971) para peneidos; y de Chávez-Alarcón y Chávez (1976) para langostinos.

De acuerdo con Teissier (1969) y Ricker (1975), la pendiente resultante de la relación logarítmica entre la longitud total y el peso total con valor igual a tres, indica que el peso específico y la forma del cuerpo son proporcionales a la talla de los ejemplares a través del tiempo. Considerando la semejanza del valor de la pendiente obtenida en este caso (3.185) con respecto a tres, se infiere que el crecimiento de M. acanthurus tiende a ser isométrico aunque en sentido estricto no suceda así, porque a pesar de la estrecha relación entre la longitud y el peso totales existen variables que afectan el peso de los organismos, como la madurez sexual y los estadios gonádicos que en términos de reproducción representan un fuerte gasto energético; otros factores importantes que influyen en el peso de los individuos son la época del año en que se colectan, así como el contenido estomacal (Ricker, 1975; Hartnoll, 1983), etc.

Por otro lado, es importante considerar que la apreciación del crecimiento isométrico de la especie tratada estará mejor definida cuando se manejen por separado las poblaciones masculina y femenina, pues éstas presentan diferencias en forma y talla, lo que puede influir en el comportamiento del modelo para la relación peso-longitud de los resultados.

Hunte y Mahon (1983) determinaron que el crecimiento de M. faustinum es de tipo alométrico al calcular valores para la pendiente de 3.15 para machos y de 3.23 para hembras.

La tendencia isométrica del crecimiento en M. acanthurus se apoya en la linealidad de la relación entre la longitud total y la longitud del cefalotórax (Fig. 3); este resultado implica que la porción anterior del organismo se mantiene proporcional a lo largo del crecimiento, ya que los juvenilesM. acanthurus tienen un cefalotórax ligeramente menor a la mitad de la longitud total del individuo, mientras que en los adultos esta sección es mayor.

El intervalo de tallas utilizado en el presente trabajo (13 a 170 mm de LT) fue considerablemente amplio, e incluyó desde organismos juveniles con escasa edad posterior a la metamorfosis hasta adultos con tallas aceptables comercialmente.

En contraste, Chávez-Alarcón y Chávez (1976) trataron individuos deMacrobrachiummayores a 40 mm; Boschi (1969) y Chávez (1973) describieron el crecimiento de camarones peneidos mayores a 50 mm de longitud total, lo que puede redundar en menor representatividad de la población.

Las tallas de M. acanthurus menores a 30 mm fueron globalmente más abundantes que las tallas posteriores, probablemente a causa de los hábitos migratorios de los individuos, como ha sido observado por Anderson (1983) paraM. ohione, y sugerido por Román (1979) y Ruiz (1988) para M. tenellum. En el presente caso es explicable la poca representación de tallas mayores al considerar la disminución de las poblaciones como resultado de la pesquería y muerte natural.

La definición de las clases de edad calculadas de acuerdo con el método de Petersen fue utilizada en sustitución de métodos directos que ayudaran a determinar con mayor precisión la edad de los organismos (Parrack, 1979).

La ausencia de algunos grupos de edad o poco representados y la superposición de modas en las,tallas son algunas de las limitantes para el empleo de este método, por lo que la representatividad de los valores modales está sujeta a comprobación al utilizar métodos como el de Cassie (1954), aunque éste no elimina apreciaciones subjetivas y conduce a resultados semejantes.

En el presente estudio la mayor limitante se produjo al tener los organismos juveniles mayor representatividad, lo que conduce a una inexacta determinación del valor de L∞, pues cuando las tallas mayores están poco representadas la línea de regresión resultante en el gráfico de FordWalford tiende a abrirse, lo que implica que el valor máximo registrado (176 mm) no representa adecuadamente la longitud total máxima hipotética (L∞), que es el valor esperado (Guzmán Arroyo, comunicación personal). Por está razón es necesario considerar que los resultados de este trabajo son de utilidad sólo como una aproximación para la descripción del crecimiento de M. acanthurus en condiciones naturales.

El ritmo de crecimiento en longitud para la especie en estudio es relativamente acelerado en las tres o cuatro primeras edades hipotéticas, en comparación con el incremento en peso que es apreciablemente más lento. Este contraste se debe a las continuas mudas de los organismos en los primeros meses de vida, entre otros factores, que promueven el crecimiento en longitud del organismo, pero simultáneamente el crecimiento ponderal se ve retardado.

El crecimiento de los individuos se vuelve asintótico a partir del tiempo teórico en el que la longitud total del organismo es de aproximadamente 200 mm y el peso oscila alrededor de 102 g (Figs. 5 y 6). El crecimiento disminuye en las edades adultas debido a que los individuos realizan mayor gasto energético en procesos diferentes a su desarrollo, como la reproducción y el mantenimiento de cuerpos cada vez mayores.

Con base en los resultados de Cruz (1968), Chávez y Rodríguez de la Cruz (1971) y Chávez (1973) para peneidos; y de Chávez-Alarcón y Chávez (1976) paraM. carcinus, y en función de las descripciones de Choudhury (1970) para juveniles de M. acanthurus, debe suponerse que cada uno de los tiempos o "edades" mencionadas en este trabajo son comparables a períodos bimestrales, por lo que se deduce que para alcanzar los valores máximos de L∞ y P∞ los individuos deberían tener una longevidad cercana a tres años.

Al respecto, Truesdale y Mermilliod (1979) calcularon períodos de vida mayor a dos años para M. ohione y Bond y Buckup (1983) hasta de treinta meses para M. botelii yM. potiuna en condiciones naturales, e infirieron adicionalmente, que M. borelii puede sobrevivir aun más tiempo en condiciones de cultivo, por lo que es posible queM. acanthurus alcance una longevidad cercana a los tres años en condiciones controladas.

Por lo anterior y a pesar del incremento en las tallas iniciales, se considera que el crecimiento deM. acanthurus es lento en comparación con otras especies, lo que se confirma al observar el valor obtenido de la constante de crecimiento (k=O.2405) (Fig. 4), ya que, de acuerdo con Beverton y Holt (1957), valores de esta magnitud indican crecimiento retardado, mientras que resultados aproximados a cinco representan crecimiento rápido.

A pesar del tiempo que transcurre para que la población M. acanthurus alcance los valores de longitud total y peso máximos, es factible que la especie llegue a alcanzar 212 mm y 106.6 g, respectivamente, pues, teóricamente, en dos años de vida algunos espéciménes alcanzarían 197 mm de longitud y 92 g de peso. Éstos son valores similares a los mencionados por Martínez (1975), que observó un ejemplar macho de M. acanthurus con 213 mm de longitud total y 89 g de peso en condiciones de cultivo.

Chávez-Alarcón y Chávez (1976) obtuvieron un gráfico de crecimiento en una población deM. carcinus suponiendo una Loo de 260 mm y tallas aproximadas a 250 mm en un lapso de. año y medio; y Lewis et al., (1966) calcularon un incremento en longitud de 20 a 110 mm en 13 ó 14 meses en la misma especie. Aunque M. carcinus es comparativamente mayor a M. acanthurus los valores calculados dan idea de las tallas que pueden alcanzar algunas especies de probada importancia económica en el géneroMacrobrachium y son útiles como patrones de referencia para efectos de acuacultura.

Tomando como parámetro los modelos de crecimiento calculados para M. acanthurus, se supone que las tallas adecuadas para la explotación comercial se logran cuando los organismos alcanzan 120 mm de longitud y 20 gramos de peso, lo que representa aproximadamente ocho bimestres de edad.

El modelo de crecimiento descrito debe considerarse como un diagnóstico del comportamiento de la población en vista de que es una representación global de la misma; si tomamos en cuenta que las hembras por lo general alcanzan tallas menores que los machos, con excepción de M. ohione,donde sucede lo contrario (Truesdale y Mermilliod, 1979; Anderson, 1983), y que ambos sexos crecen a velocidades similares durante los primeros meses de vida (Lewiset al.,1966; Chávez-Alarcón y Chávez, 1976), pero en forma retardada posteriormente; los modelos de crecimiento propuestos en este trabajo describen la población conjunta de machos y hembras, por lo que es conveniente realizar cálculos por separado, lo cual pudiera dar valores ligeramente diferentes.

1. La reproducción de M. acanthurus en el sistema palizada Boca Chica se lleva a cabo durante todo el año, con un claro incremento durante el período lluvioso.

2. Es probable que la mayor incidencia de hembras se deba a una mayor permanencia en el área con fines reproductivos y a la captura selectiva de los machos de tallas mayores ejercida por los pescadores.

3.Macrobrachium acanthurus se reproduce en el área estudiada a longitudes mínimas de 35 mm.

4. Existe una relación directamente proporcional entre la longitud de las hembras y su fecundidad; el porcentaje en peso de la masa ovigera es proporcional en la mayoría de los casos a la longitud total de las hembras.

5. El número máximo de huevecillos que teóricamente puede producir una hembra en la población (28,000) excede considerablemente a la cantidad observada (14,840) en el estudio, probablemente se debe a que no se contabilizó toda la masa ovígera y a que durante el manejo las hembras pueden perder parte de los huevos.

6. La relación entre el peso y la longitud es potencial; su comportamiento se define mediante la ecuación P= 4.15 x 10 ^-6 L 3.185, que es un valor análogo al presentado por otros decápodos.

7. Los valores de los parámetros calculados para el desarrollo del modelo de von Bertalanffy son:

Constante de crecimiento:k = 0.2405

Longitud máxima teórica:L∞ = 212.06 mm

Peso total máximo teórico:P∞ = 106.6g

El tiempo teórico inicial de crecimiento es: to = -0.86, por lo que las ecuaciones de crecimiento para la población deM. acanthurus se expresan como: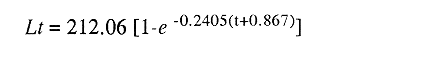

mientras que para el peso: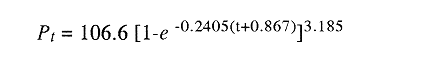

8. El valor de la constante de crecimiento (3.185) sugiere un incremento isométrico en los organismos, aunque en sentido estricto el valor dek es diferente de tres.

9. La tendencia de crecimiento isométrico en M. acanthurusse apoya en la relación lineal observada entre la longitud total y la longitud del cefalotórax, cuya expresión matemática es:LC = 0.4897 (LT) + 0.998.

10. Las edades utilizadas en las ecuaciones de crecimiento son comparables a períodos bimestrales, por lo que se considera que el crecimiento deM. acanthurus es lento en relación con otras especies.

Los autores agradecen el apoyo económico que brindó el CONACyT mediante el Convenio PCECBNA-021923 entre éste y el ICMyL-UNAM; así como a dos árbitros anónimos y al Sr J. L. Orozco Ampudia, Editor de la revista, cuyas recomendaciones ayudaron a mejorar este trabajo.

Cerrar esta ventana