SOLUCIÓN DE LA ECUACIÓN DIFERENCIAL DE CRECIMIENTO EN PESO, DE VON BERTALANFFY (1938), POR DOS MÉTODOS DISTINTOS

Trabajo recibido el 17 de junio de 1992 y aceptado para su publicación el 28 de julio de 1993.

RESUMEN

INTRODUCCIÓN

En pesquerias, el estudio del crecimiento de los organismos es uno de los temas de investigación de mayor importancia. Varios han sido los autores que mediante métodos matemáticos han tratado de describir el crecimiento animal; entre ellos, von Bertalanffy (1938) es quien ha logrado desarrollar la formulación matemática que mejor satisface ciertas condiciones primordiales, como son, por ejemplo, que: a) la ecuación matemática sea coherente con el proceso biológico del crecimiento, b) la formulación se pueda incorporar fácilmente en los modelos de dinámica de poblaciones y de administración de recursos pesqueros, y, lo más importante, c) la ecuación se ajuste bien a la mayor parte de los datos observados acerca de crecimiento en peces (Csirke, 1980).

La ecuación que describe el crecimiento en longitud está dada por: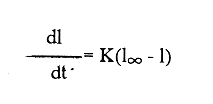

(1)

que es una ecuación diferencial lineal cuya solución se calcula fácilmente por el método de separación de variables. La solución de (1), conocida como ecuación de crecimiento en longitud, de von Bertalanffy, está dada por: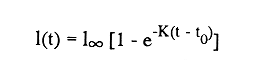

(2)

donde

l(t): denota la longitud del pez a la edad t.

l∞: es una constante, que representa la longitud asintótica o la longitud teórica máxima que el pez puede alcanzar cuando t tiende a infinito.

K: representa la constante de crecimiento.

t: representa la edad.

t₀: es la edad teórica a la cual la longitud del pez debe ser cero.

La expresión análoga para el crecimiento en peso (W) no se obtiene mediante una solución directa de una ecuación diferencial; ésta se calcula al sustituir la expresión (2) en la ecuación que relaciona el peso con la longitud (W= aL^b, donde a y b son constantes), lo cual da: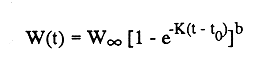

(3)

W∞ representa el peso asintótico. En el caso de crecimiento isométrico, b toma el valor de 3.

La determinación de las ecuaciones de crecimiento en peso y longitud se reduce al cálculo de los parámetros: l∞, W∞, K y t₀. Para su estimación existen varios métodos; entre ellos se encuentran los desarrollados por Ford (1933), Walford (1946), Gulland (1964), Tomlinson y Abramson (1961), Allen (1966) y Beverton (1954).

La metodología mencionada en el párrafo anterior se ha utilizado extensamente en varias regiones para diferentes especies, como: Sardina pilchardus (Larrañeta, 1965); Thunnus thynus (Rodríguez-Roda, 1964); Phycis blenoides (Gallardo, 1986) y Limanda limanda (Ortega, 1988).

El presente trabajo se enfoca principalmente a resolver la ecuación diferencial de crecimiento en peso por el método de Variables Elegantes. Este método se usa comúnmente en la solución de ecuaciones diferenciales y se ha aplicado en algunos modelos clásicos en Ecología (Sánchez, 1989); de modo particular se aplicó para resolver la ecuación de crecimiento alométrico de longitud (Aguilar et al., 1984). En el Apéndice se incluye un procedimiento alterno para resolver la ecuación diferencial de crecimiento en peso por el método de Leibnitz (Boyce y Di Prima, 1979). Así mismo, se desarrolla la metodología necesaria para el cálculo de los parámetros del modelo de crecimiento a partir de datos observados de peso, longitud patrón, altura y edad. Por último, la metodología anterior se aplica a la lisa blanca: Mugil curema.

La ecuación para el crecimiento isométrico: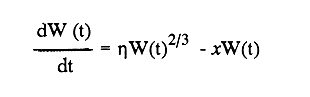

(4)

está basada en hipótesis que reflejan básicamente que la densidad y la forma de un organismo se mantienen esencialmente iguales dentro de su ciclo de vida, aunado a que el aumento de peso por unidad de tiempo se debe al ritmo de anabolismo-catabolismo, y que el ritmo de anabolismo es proporcional a la superficie del organismo (Aguilar et al., 1984).

Un caso más general de la ecuación (4) es el siguiente: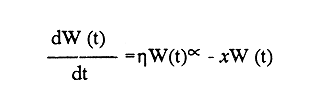

(5)

donde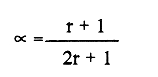

ηy x representan las tasas de metabolismo, r es el exponente de la relación entre la anchura (altura) y la longitud del organismo: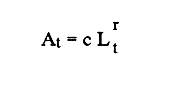

(6)

Cabe mencionar que para el caso isométrico r = 1. Los parámetros de la ecuación (6) se pueden determinar mediante una transformación logarítmica:

ln A_t = ln c + r ln L_t (7)

A partir de (5) se determina el peso asintótico: W∞ = (η/x) ^1/Β, donde Β = r/(2r+ 1), bajo la condicion: α + Β= 1.

Al introducir este parámetro en la ecuación (5) se obtiene: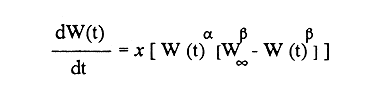

(8)

Para resolver la ecuación (8) se considera la existencia de una Variable Elegante, dada por: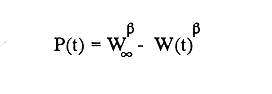

(9)

que transforma la ecuación (5) en un modelo de tipo malthusiano, de fácil solución. La demostración se basa en la derivación con respecto a t· de la variable introducida (9), de manera conjunta con la ecuación (8); la expresión resultante es: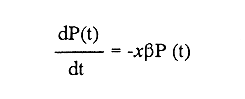

(10)

cuya solución está dada por: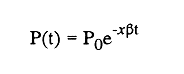

(11)

donde P₀ = W^Β∞- W^Β₀;W₀ representa el peso al tiempo t=0. Al igualar (11) con la expresión (9) y resolviendo W(t) se obtiene la solución de la ecuación (5):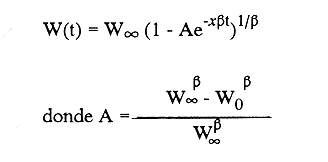

(12)

Es oportuno mencionar que es la misma expresión que se obtiene al resolver (5) por el método de Leibnitz (Apéndice). En (12) aparecen tres parámetros: W∞, A y x, de fácil determinación mediante regresiones lineales. Para obtener la primera, basta evaluar la ecuación (12) a la edad t + l; obteniendose: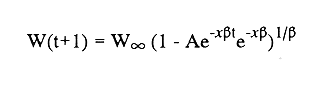

(13)

que al elevar al exponente Β y sumar-restar el término W^Β_∞ e ^-xΒ se obtiene la expresión siguiente: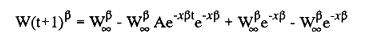

(14)

la cual, después de un poco de álgebra, da como resultado: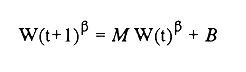

(15)

donde M = e^-xΒ y B = (1 - e^-xΒ) W^Β∞, los cuales se pueden determinar por mínimos cuadrados. A partir de la pendiente y de la ordenada al origen, se obtienen los valores de x y W^Β∞: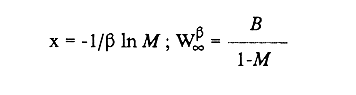

(16)

El parámetro A de la ecuación (13) se determina a partir de una segunda regresión lineal. Después de hacer algunas operaciones algebraicas en (13), se tiene que la regresión mencionada está dada por: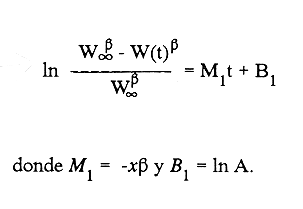

(17)

Es importante señalar que las regresiones lineales (15) y (17) son válidas para el crecimiento en general, el isométrico es un caso particular, en el cual r = 1 y Β = 1/3, cuyas regresiones correspondientes son:

W(t + 1)^1/3 = M W(t)^1/3 + B (18)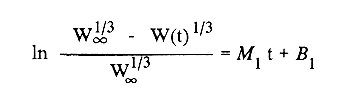

(19)

donde M₁ =e^-k/3 ; B = (1-e ^-k/3)W∞; M ₁ = -x/3 y B₁=In A

La metodología anterior se aplicó a la lisa blanca (Mugil curema) [Villaseñor y Jurado, comunicación personal]. El crecimiento en longitud se determinó usando la ecuación de von Bertalanffy. Para determinar L∞, x y t₀ se usó el método de Ford (1933) y Walford (1946). La ecuación resultante es:

L_t = 338.49 [1 - e ^{-0.341 (t + 1.117)}] (20)

El resultado para la relación peso-longitud, calculada a partir de los datos respectivos de peso y longitud fue:

W=(8.64 X 10_-5)L ^2.59 (21)

El crecimiento en peso a partir de la ecuación de von Bertalanffy utilizando la relación anterior (21), quedó expresada como:

Wt = 307.69 [1 - e^{-0.341 (t + 1.117)}] ^2.59 (22)

Los datos de longitud patrón, altura, edad y peso también se utilizaron para calcular las constantes del modelo por el método de Variables Elegantes. La determinación de los parárnetros se llevo a cabo con las ecuaciones (15) y (17), que dio como resultado la ecuación siguiente:

W(t) = 531.7 [1 - (066) e ^{- (0.17)t}] ^2.59 (23)

En la tabla I se presentan los valores de peso observados (que representan valores promedio con distribución normal), así como los calculados a partir de (22) y (23) para la lisa blanca (Mugil curema); se nota que en general las estimaciones calculadas con la ecuación (23) muestran una menor desviación de los valores observados.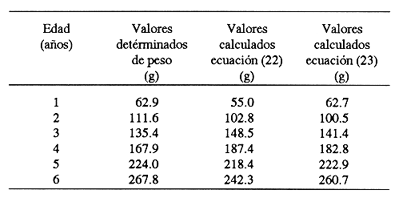

TABLA 1. Comparación de los pesos calculados y determinados para la lista blanca (Mugil curema)

La tabla II contiene los porcentajes de error en la estimación para las ecuaciones mencionadas: (22) y (23). Para la ecuación (22) el porcentaje varía de un mínimo de 2.5 a un máximo de 12.56%; en el caso de la ecuación (23) se observa una variación menor: de 0.31 a 9.94%.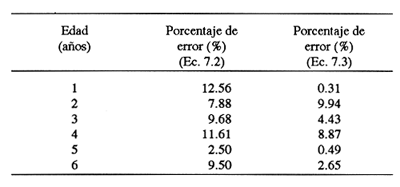

TABLA II Valores de los porcentajes de error en los cálculos mediante las ecuaciones (22) y (23)

En las tablas III y IV se observan los resultados de las regresiones lineales para la determinación de A, W∞^1/b y x. La ecuación 15 resultó altamente significativa (r = 0.971, r² = 0.944 y p = 0.006). De la misma manera, para la ecuación 17 se obtuvo un coeficiente de correlación muy alto (r = 0.992) y un porcentaje de variación explicada alta (r² = 0.985); así mismo, el análisis de varianza indica que las pruebas son significativas (p = 0.006 y p = 0.0001).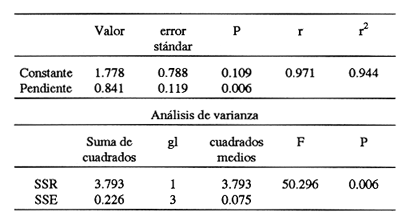

TABLA III Resultados de la regresión (Ec.15) para obtener los parámetros del modelo de crecimiento en peso por el método de variables elegantes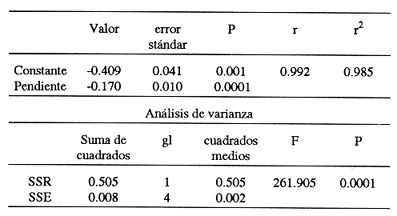

TABLA IV Resultados de la regresión (Ec.17) para obtener los parámetros del modelo de crecimiento en peso por el método de variables elegantes

La figura 1 muestra el comportamiento de la solución para el caso de crecimiento en peso, de von Bertalanffy, cuya forma es sigmoidea y, con excepción del último punto, la curva se ajusta bien a los datos observados. En la figura 2 se observa el comportamiento de la solución de la ecuación diferencial para el crecimiento en peso, de von Bertalanffy, por el método de Variables Elegantes (ecuación 23), cuyos parámetros se obtienen mediante las fórmulas (15) y (17); su forma es nuevamente sigmoidea, se observa que la curva se ajusta bastante bien a todos los puntos; sin embargo, a partir de estas dos gráficas es difícil decidir cual se ajusta mejor a los datos observados. Una comparación cualitativa se presenta en la figura 3, donde se gratificaron los valores observados y los calculados a partir de las ecuaciones mencionadas. En ella se nota que, a excepción de la edad 2, todos los valores estimados con (23) se encuentran más cercanos a los observados.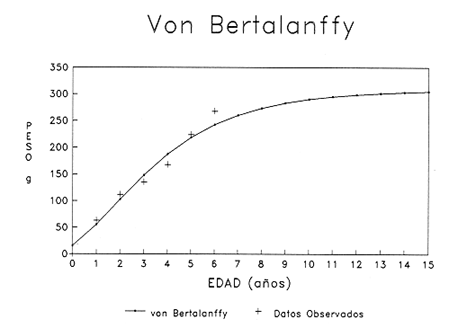

Figura 1. Comportamiento de la solución para el caso de crecimiento en peso obtenida mediante una transformación directa que relaciona el peso con la longitud (Ec.de von Bertalanffy).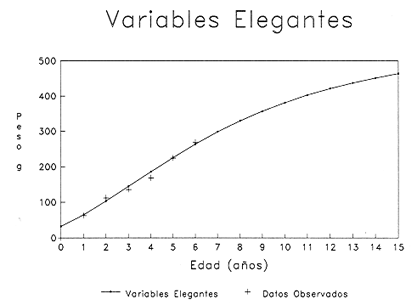

Figura 2. Comportamiento de la solución de la ecuación diferencial de crecimiento en peso, de von Bertalanffy [Ec.(23)]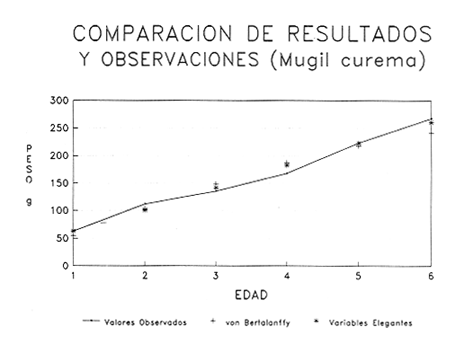

Figura 3. Comparación de los pesos calculados y observados para la lisa blanca (Mugil curema).

Para una comparación cuantitativa se usaron los criterios propuestos por Roff (1983): el error cuadrático medio (Neter et al., 1990) y el error porcentual absoluto medio (Roff, 1983). La tabla V contiene los valores de las cantidades mencionadas; se advierte que en ambos casos los valores más bajos corresponden a la ecuación (23).

TABLA V. Resultados del error cuadrático medio y del error porcentual absoluto medio para las ecuaciones (22) y (23)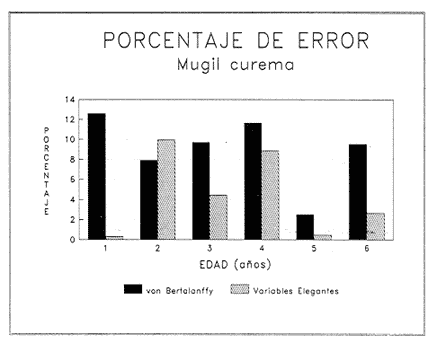

Figura 4. Porcentaje de error en el cálculo de pesos mediante las ecuaciones (22) y (23).

La ecuación (23) obtuvo el valor más bajo de error cuadrático medio (432.68); por lo anterior, bajo los criterios establecidos por Roff (1983), se puede considerar que para el caso de los datos de la lisa blanca aquí tratado, el mejor modelo es el representado por la ecuación (23). En cuanto al valor práctico de los modelos, ambas ecuaciones [(22) y (23)] obtuvieron un valor por abajo del mínimo aceptable (20%) propuesto por Roff (1983); además cabe señalar que también en este aspecto, el valor más bajo de Error Porcentual absoluto medio corresponde a la ecuación (23).

Como se ha mostrado, el método de Variables Elegantes y el de Leibnitz son procedimientos adecuados para solucionar la ecuación diferencial de crecimiento en peso. La solución obtenida es un modelo de crecimiento de naturaleza no lineal. Los párametros del modelo se pueden calcular fácilmente a partir de tres regresiones lineales. Por otra parte, cabe mencionar que la ecuación desarrollada es de carácter general, por lo que el caso isométrico es un caso particular del modelo propuesto.

Al aplicar los modelos de von Bertalanffy y el propuesto en este trabajo a datos de la lisa blanca (Mugil curema), se observó que bajo los criterios propuestos por Roff (1983) el modelo propuesto presenta mejor ajuste, incluso en los valores extremos y, además, constituye un método práctico para la determinación del crecimiento en peso. Sin embargo, es necesario validar el modelo aplicándolo a otras especies de organismos marinos y dulceacuícolas.

En el presente apéndice se resuelve la ecuación diferencial de crecimiento en peso por el método de Leibnitz (Boyce y di Prima, 1979).

La ecuación diferencial de crecimiento: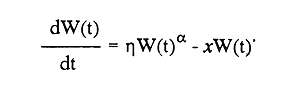

(1)

se puede reescribir de la manera siguiente: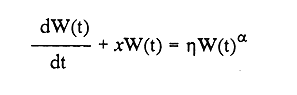

(2)

que al dividir entre W(t)^α adopta la expresión siguiente: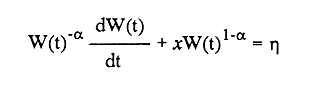

(3)

Para linealizar la ecuación anterior se propone el siguiente cambio de variable: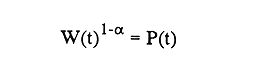

(4)

Si se calcula la derivada de la expresión anterior se obtiene: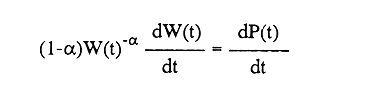

(5)

al despejar: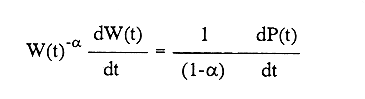

(6)

si se sustituyen las expresiones (4) y (6) en la ecuación (3), se obtiene la ecuación diferencial siguiente: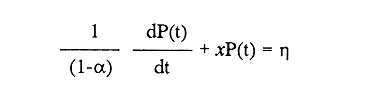

(7)

que se puede escribir como: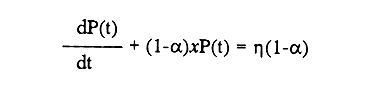

(8)

si los valores Β = (1-α) y η = xW^Β∞ se sustituyen en la ecuación (8), se llega a la expresión siguiente: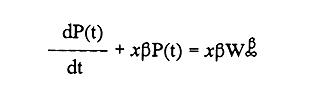

(9)

que es una ecuación diferencial lineal de primer orden, no homogénea, y que se puede resolver con ayuda del factor integrante µ = e ^xΒt, cuya solución es: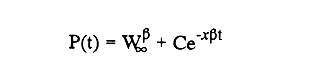

(10)

Para determinar el valor de la constante C se considera la condición inicial: P(0) = W(0) ^1-α= W₀^1-α con W₀ = peso inicial; la expresión resultante es: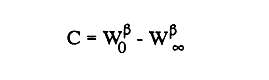

(11)

usando (4), (10) y (11) se obtiene: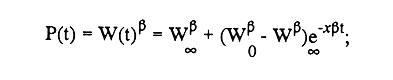

después de un poco de álgebra, la solución puede escribirse como: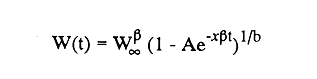

(12)

con A = -C/W^Β∞; como se observa, la expresión obtenida es la misma que se obtuvo con el método de Variables Elegantes.

Aviso de Privacidad

Cerrar esta ventana