ANÁLISIS DE LAS FRECUENCIAS DE TALLAS POR MEDIO DE LOS MÉTODOS DE PETERSEN, CASSIE Y BHATTACHARYA, PARA LA DETERMINACIÓN DE LA EDAD DE LA BRÓTOLA PHYCIS BLENNOIDES (BRUNNICH 1768) EN EL MEDITERRÁNEO OCCIDENTAL (PISCES: GADIDAE)

Trabajo recibido el 22 de julio de 1984 y aceptado para su publicación el 12 de noviembre de 1984.

RESUMEN

INTRODUCCIÓN

La determinación de la edad mediante el análisis de frecuencias de tallas de una población, fue utilizada inicialmente por Petersen (1892); se basa en la suposición de que en un mes o estación del año, las tallas de los peces, pertenecientes a los diferentes grupos de edad, tienden a presentar una distribución normal. Así, al representar gráficamente la distribución de las frecuencias de tallas de una población, se muestra una serie de máximos modales que puede interpretarse como la talla media de los peces a una edad determinada. Estudiando el movimiento de estas clases modales a lo largo de un año, podemos tener una idea del crecimiento.

Un avance sobre el método de Petersen, lo constituyen las técnicas propuestas por: Harding, 1949; Cassie, 1950, 1954, 1963; y Bhattacharya, 1967. Dichas técnicas tienden a discriminar las sobreposiciones de las distribuciones normales y ayudan a interpretar los histogramas de que se dispone.

Harding (1949), realizó una aplicación de este método al estudio de las distribuciones de frecuencias polimodales. Cassle aplica esta técnica eliminando algunos errores del método original, referentes a la sobreposición de puntos de las distribuciones de frecuencias que componen la curva polimodal.

Bhattacharya (1967), propone un método para separar las sobreposiciones de los elementos de las distribuciones normales, mediante el análisis de la frecuencia observada.

Este autor desarrolla su método, basándose en las técnicas empleadas por Buchanan-Wollasten y Hodgeston (1929); Oka (1954) y Tanaka (1962), que consideran al logaritmo de las frecuencias de tallas como una función cuadrática del punto medio de la clase.

Por otra parte, para la obtención gráfica de las líneas rectas que representan los componentes de la curva de Gauss -a partir de las cuales, obtiene las longitud media y la desviación estándar, Bhattacharya emplea las diferencias de los logaritmos de las frecuencias de tallas de dos clases consecutivas.

Se obtuvo la longitud total de 5,397 ejemplares de Phycis blennoides, procedentes de los muestreos biológicos y de la captura comercial, de septiembre de 1976 a septiembre de 1978.

Los ejemplares se obtuvieron en el Mediterráneo occidental frente a las costas de Cataluña, entre Blanes y Vilanova i la Geltrú, de profundidades que oscilaron entre 150 y 650 m.

Los muestreos de la captura comercial se efectuaron varias veces a la semana y una vez al mes se realizó un muestreo biológico, efectuando arrastres a distintas profundidades: el primero entre 150 y 300 m, el segundo entre 300 y 400 m, y el tercero entre 400 y 600 m, utilizando para ello una red comercial (bou) con un copo de 35 mm y un sobrecopo de 10 mm de abertura de malla.

Los ejemplares fueron separados, de acuerdo con las profundidades en que fueron capturados y conservados, en una cámara frigorífica a una temperatura de -10°C.

Para obtener las mediciones se utilizó un ictiómetro IIP, colocándose el ejemplar sobre el costado derecho para determinar su longitud total, ésta se midió al centímetro más próximo, desde la punta del hocico hasta el extremo final de la aleta caudal.

Los grupos de edad para esta especie, fueron establecidos por Gallardo-Cabello (1979).

Para el análisis de las frecuencias de tallas, se aplicaron los métodos de Petersen (1892), Cassie (1950, 1954, 1963) y Bhattacharya (1967).

En las figuras 1 y 2, se muestran las frecuencias, en porcentaje, del número de individuos correspondientes a las diferentes clases de tallas.

El período de máxima freza ha sido determinado para el mes de julio y, por lo tanto, se considera este mes como la fecha de nacimiento de la nueva generación, que inicia su aparición en las capturas durante el mes de abril (Gallardo-Cabello, 1979).

En las figuras 1 y 2 y en la Tabla 1, se muestra la evolución a lo largo del tiempo, de la moda correspondiente a la clase anual "0", es decir a la nueva generación, siendo un poco menos precisas las variaciones de las modas correspondientes a las edades restantes.

Se puede apreciar de esta manera, que en el mes de abril (1977-78), se ve una primera moda a los 80 mm, correspondiente a los ejemplares que aún no han cumplido su primer año de edad, y una segunda moda a los 170 mm, perteneciente a los individuos que han alcanzado su primer año de vida, y así sucesivamente.

En el mes de julio, la primera moda aparece a los 130 mm y corresponde a la edad "0", que en este mes se convierte en la clase anual "1"; la segunda moda aparece a los 190 mm, indicando el paso de la clase anual "1" a la clase anual "2". Las edades "3", "4" y "5" están representadas en este mes por las modas que aparecen a los 220, 240 y 270 mm, respectivamente.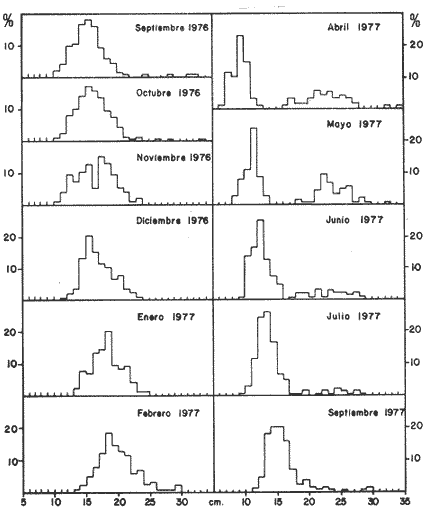

Fig. 1. Histogramas mensuales de las distribuciones de frecuencia de tallas de Phycis blennoídes (septiembre de 1976 a septiembre de 1977).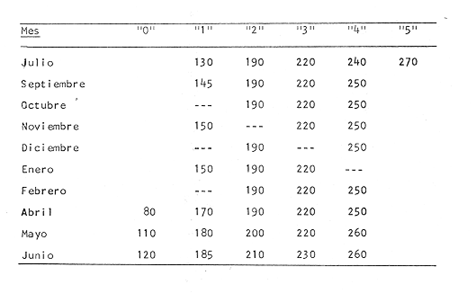

TABLA 1 TALLAS MODALES PARA CADA GRUPO DE EDAD A LO LARGO DEL AÑO DE 1977. TALLA EN MM PARA CADA CLASE ANUAL

En los meses correspondientes a 1976 y 1978, se observan valores semejantes a los obtenidos para los meses del año de 1977.

De esta forma, el análisis de frecuencias de tallas, mediante el Método de Petersen, permite una apreciación de las tallas correspondientes a los distintos grupos de edad, siendo además posible observar que el crecimiento se lleva a cabo durante la primavera, disminuyendo durante los meses de otoño e invierno.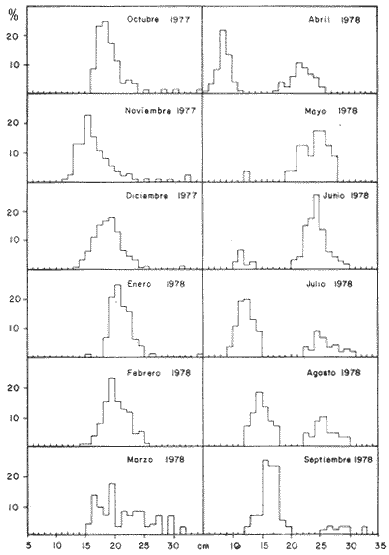

Fig. 2. Histogramas mensuales de las distribuciones de frecuencias de tallas de Phycis blennoides (octubre de 1977 a septiembre de 1978).

En la Tabla 2, se muestran las tallas pertenecientes a cada clase anual, correspondiendo a la clase anual "0" la talla alcanzada durante el mes de abril, en que la nueva generación de brótola cumple 8 meses de edad. Asímismo, se presentan las tallas alcanzadas durante el mes de julio, para las clases anuales restantes.

El método de Petersen, presenta algunas inexactitudes para la determinación de la edad de los peces.

En Phycis blennoides el crecimiento es más intenso durante sus primeras etapas de desarrollo por lo que en los ejemplares de las clases anuales "0", "1" y "2" hay una manifiesta diferencia en longitud, lo que no ocurre en los peces de mayor edad, produciéndose a partir de la clase anual "4", superposiciones entre los máximos modales que impiden la determinación de clases anuales superiores a "5".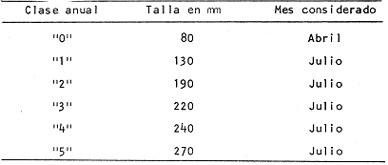

TABLA 2 TALLA PARA CADA GRUPO DE EDAD DETERMINADA POR EL MÉTODO DE PETERSEN

Sin embargo, para un examen previo de la composición de tallas de la población, el método resulta adecuado, ya que se dispone de una base firme para el estudio posterior de la edad, y para el reconocimiento de las tallas de las primeras edades.

Para la aplicación de este método, se han elegido las frecuencias de tallas correspondientes al mes de julio de 1977, por ser el período de máxima freza y nacimiento de la nueva generación.

En la figura 3, se muestra la distribución de los porcentajes acumulativos correspondientes a 287 ejemplares. Los puntos de inflexión corresponden a 93.3, 94.9, 97.3 y 99.3 %.

Para obtener la longitud media y la desviación estándar de la edad "0" –que no está representada en la distribución de tallas del mes de julio, por ser la época en que las brótolas más jóvenes cumplen su primer año de edad–, se ha aplicado este método a los datos obtenidos para el mes de abril de 1977, período en que éstas aparecen en las capturas.

La distribución del mes de abril aparece en la figura 4. En ella se distinguen dos inflexiones que corresponden al 63. 1 y 77.4 %, obteniéndose para la clase de edad "0" una talla media de 83 mm y una desviación estándar de 10 mm; y para la clase de edad "1", una talla media de 175 mm y una desviación estándar de 9 mm. Los resultados obtenidos aparecen en la Tabla 3.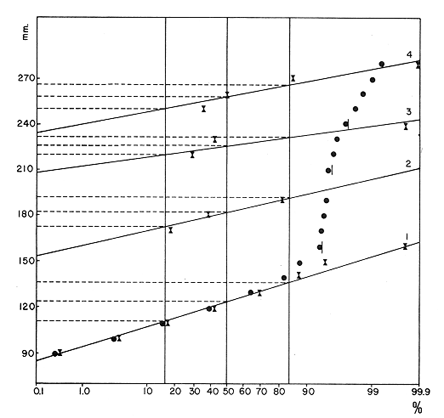

Fig. 3. Análisis por medio del papel de probabilidades dé la distribución de frecuencias de tallas del mes de julio de 1977 de Phycis blennoídes.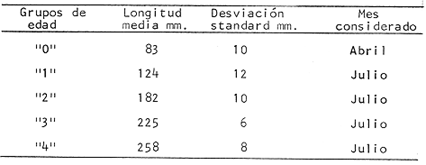

TABLA 3 TALLA PARA CADA EDAD DETERMINADA POR EL MÉTODO DEL PAPEL DE PROBABILIDADES

El método de Cassie puede resultar adecuado y proporcionar buenos resultados para el estudio de la determinación de la edad. Sin embargo, en el análisis de algunas poblaciones de peces, como es el caso de la brótola del Mediterráneo occidental, se pueden presentar algunas estimaciones erróneas.

Las curvas obtenidas por medio de este método dependen, muy estrictamente, de la determinación del lugar que ocupan los puntos de inflexión, los cuales suelen aparecer con muy poca claridad, resultando más práctico, en muchas ocasiones, revisar y comparar el histograma original de frecuencias de tallas, que localizar los puntos de inflexión sobre el papel de probabilidades.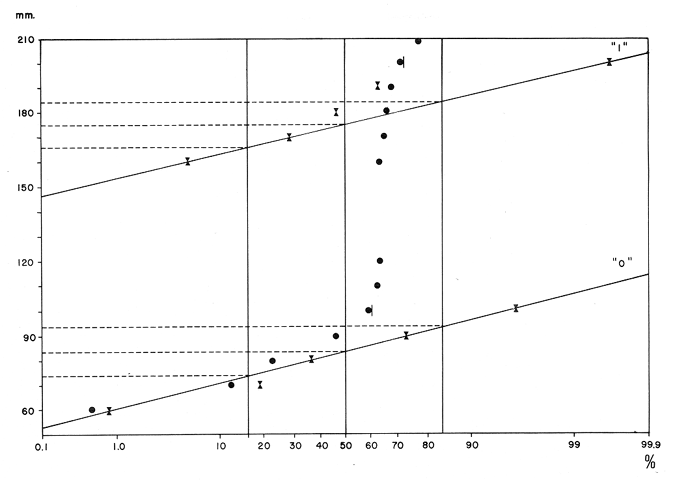

Fig. 4. Análisis por medio del papel de probabilidades de las frecuencias del mes de abril de 1977 de Phycis blennoides.

La bondad del ajuste de esta técnica, depende de la claridad con que se presenten las curvas polimodales obtenidas en los histogramas de Petersen.

Este método se aplicó para analizar la distribución de las frecuencias de tallas, correspondientes al mes de julio de 1977. Los datos utilizados para dicho análisis también fueron aplicados en el papel de probabilidades.

En la figura 5, se muestran las diferencias logarítmicas de las frecuencias de clases de tallas, con respecto al punto medio de cada clase de talla, obteniéndose 5 líneas rectas, con pendiente negativa.

Aplicando el método anterior a la distribución de frecuencias de tallas del mes de abril de 1978 –período en que los ejemplares de Phycis blennoídes, pertenecientes a este grupo de edad aparecen en las capturas–, se obtuvieron la longitud media y la desviación estándar de la edad "0".

En la figura 6, Δ Log₁₀ y vs x, se muestra la alineación de puntos y la recta obtenida. En la Tabla 4, se muestran los resultados obtenidos por medio de este método para las edades de 0 a 5 años.

El método de Bhattacharya puede ser útil en la determinación de la edad, siempre y cuando los intervalos de las clases de tallas que se escojan sean pequeños y las frecuencias de cada clase estén bien representadas.

Las deficiencias de este método, se presentan en la obtención gráfica de las líneas rectas, ya que en ocasiones se observa la dispersión de algunos puntos, los cuales no se pueden alinear, resultando difícil establecer un criterio objetivo, sobre cuales puntos deben considerarse para trazar las líneas rectas. El problema puede acentuarse cuando se observan superposiciones, debido a que los componentes de la distribución no están lo suficientemente espaciados en el eje de las abscisas. Lo anterior puede dar lugar a graves errores en la estimación de la longitud media.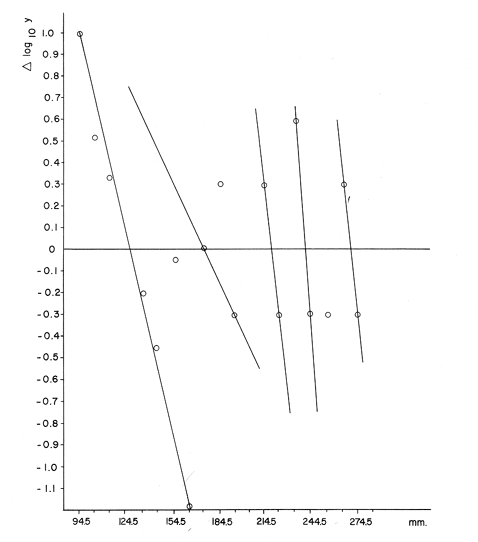

Fig. 5. Distribución de frecuencias de tallas de Phycis blennoides durante el mes de julio de 1977 (método de Bhattacharya).

Los histogramas obtenidos por medio del método de Petersen son bastante claros, pero el método de Bhattacharya puede resultar más rápido y simple que los propuestos por otros autores.

Los valores de las tallas para cada edad, calculados mediante los métodos anteriores, aparecen en la Tabla 5. Dichos valores han sido comparados con los datos obtenidos de la lectura de los otolitos mediante la suma de los cuadrados de las diferencias.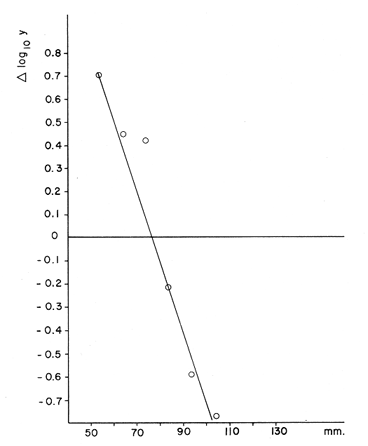

Fig. 6. Distribución de frecuencias de tallas de Phycis blennoides durante el mes de abril de 1977 (método de Bhattacharya).

A continuación se analizan los métodos aplicados.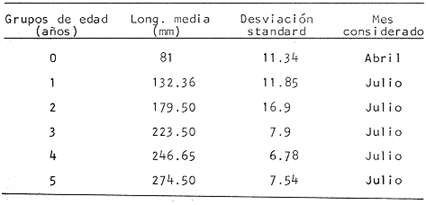

TABLA 4 TALLA PARA CADA EDAD DETERMINADA POR MEDIO DEL MÉTODO DE BHATTACHARYA

El valor de la longitud media en la edad "0" obtenido por este método fue igual al observado por la lectura de otolitos, (Tabla 5). Los resultados fueron similares para la edad "1". Sin embargo, a partir de la edad "2" las diferencias de las longitudes medias obtenidas por estos dos metodos, oscilan entre 5 y 13 mm.

El sistema de Petersen permitió la identificación de seis grupos de edad, mientras que el examen de los otolitos permitió establecer ocho grupos. Esto se debe a que los histogramas de Petersen presentaron superposiciones entre los máximos modales, a partir de la edad "5", impidiendo determinar más de seis grupos de edad.

Este método permitió a partir de los datos de Petersen, obtener valores más cercanos a los determinados por medio del examen de los otolitos. Sin embargo, sólo permitió afinar algunos valores, y no la totalidad de los mismos.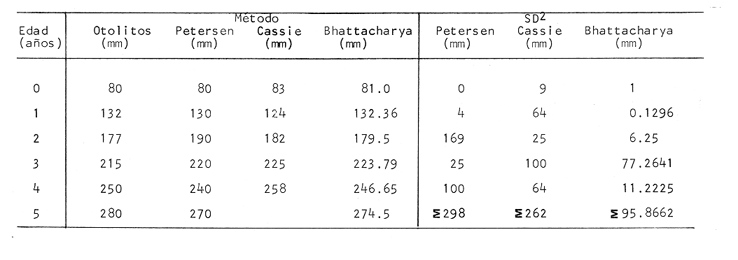

TABLA 5 VALORACIÓN DE LOS MÉTODOS EMPLEADO

La técnica de Cassie, no permitió determinar el grupo de edad "5" obtenido por el método de Petersen. Lo que indica mayor. imprecisión en comparación con los otros métodos.

Los valores obtenidos para la determinación de la edad de Phycis blennoides al aplicar este método, resultaron ser los más próximos a los determinados mediante la lectura de los otolitos. Así, el proceso de separación de las sobreposiciones polimodales, desarrollado por ese autor, resultó ser más rápido, sencillo y adecuado que el propuesto por Cassie.

Los resultados obtenidos por los métodos descritos pueden ser adecuados para determinar las tallas de los primeros grupos de edad. Dichos métodos pueden compararse con los logrados mediante la lectura de los otolitos, siendo ambos indispensables para estudiar el crecimiento durante sus primeras etapas.

De los diferentes métodos empleados durante el análisis de las frecuencias de las tallas mensuales Petersen, 1892; Cassie, 1950, 1954 y 1963, y Bliattacharya, 1967, este último proporcionó los resultados más próximos a los determinados por la lectura de los otolitos.

Las tallas obtenidas para cada grupo de edad por el método de Bliattacharya son las siguientes:

Los histogramas de Petersen demostraron que los individuos de cada generación, nacidos durante los meses de julio y agosto, aparecen en el bentos en abril y mayo con una talla modal de 80 mm.

A Ramón Margalef, catedrático de ecología de la Universidad Central de Barcelona, por la revisión del presente trabajo. A Jaime Rucabado, Conchita Allué y Pilar Sánchez, miembros del grupo de Recursos del Instituto de Investigaciones Pesqueras de Barcelona. A Alfredo Laguarda-Figueras, investigador del Instituto de Ciencias del Mar y Limnología de la Universidad Nacional Autónoma de México por su apoyo y estímulo para la publicación del presente. A Alicia Durán González, del Instituto de Ciencias del Mar y Limnología, quien amablemente elaboró los dibujos de este trabajo.

Aviso de Privacidad

Cerrar esta ventana