MODELO DE RELACIÓN TRÓFICA ENTRE MOLUSCOS, EQUINODERMOS Y CRUSTÁCEOS DE LA COMUNIDAD BENTÓNICA DE LA COSTA NOROCCIDENTAL DE BAJA CALIFORNIA, MÉXICO

Trabajo recibido el 10 de octubre de 1980 y aceptado para su publicación el 4 de mayo de 1981.

RESUMEN

INTRODUCCIÓN

Esta zona de la República tiene un sin número de pesquerías que a través del tiempo han ido incrementándose en volumen de captura, ocupando así, mano de obra regional en gran escala y expandiendo sus actividades sobre los mantos de sargazo (Macrocystis pyrifera), y la comunidad bentónica adyacente a estos, los que según Fralick y Ryther (1976), es la especie dominante y habitat del ecosistema local. Como ejemplo de esta expansión, se tiene el desarrollo de la nueva pesquería de erizo, basada en el erizo rojo (Strongylocentrotus franciscanus), y en el erizo púrpura (Strongylocentrotus purpuratus); la cual comenzó en el año de 1960, cerrándose poco después por el alto costo de la mano de obra, y la falta de demanda en el mercado internacional; pesquería que fue reabierta en 1971 por la empresa PROMEX, exportándose toda la producción al Japón (Pineda, 1973).

La importancia del manejo racional de esta comunidad no es tan sólo económico, sino también ecológico, puesto que el papel que juega Macrocystis pyrifera es muy importante para otras asociaciones de algas de la comunidad como son:Egregia laevigata, Cystoseira osmundacea, Chorallina chilensis, Eisenia sp y Laminaria sp, las que junto conMacrocystis, mantienen toda una comunidad importante para el hombre a nivel económico-ecológico, ya que las especies más valiosas son las que viven ahí, como la langosta roja (Panulirus interruptus), el abulón amarillo (Haliotis corrugata), el abulón negro (Haliotis cracherodii), el erizo rojo (Strongylocentrotus franciscanus) y el erizo púrpura (Strongylocentrotus purpuratus); reciben la presión de pesca.

Otras especies importantes también por el papel que desempeñan, como competidores y depredadores en la comunidad son las siguientes: erizo, Lytechinus variegatus (competidor del género Strongylocentrotus); cangrejo.Cancer antennarius y C. productus (como depredadores de erizo, competidores de langosta, y susceptibles de nueva pesquería); pez cabeza de borrego,Pimelometopon pulchrum (depredador de erizo); "pez señorita",Oxyjulis californica, según Tegner (1976), (depredador de erizo en estadios juveniles); pez,Scorpaenichtys marmoratus (depredador de abulón); y las estrellas de mar:Pycnopodia helianthoides yPisaster ochrecea como depredadores de erizo y abulón. (Connel y Schroeter 1975; Dayton y Connel, 1977).

Macrocystis, es la fuente más importante de algina, coloide utilizado en la industria alimenticia como estabilizador (Fralick y Ryther, 1976), por lo que requiere un adecuado manejo, pues de no ser así, el ecosistema puede desequilibrarse, perdiéndose con ello las pesquerías antes señaladas, como la de langosta y abulón (reservadas a sociedades cooperativas), en cambio se incrementaría la de erizo (concedida a permisionarios), la cual se vendría abajo al decaer la productividad primaria por sobrepastoreo y sobreexplotación.

Fenómeno que cae dentro de la teoría del análisis de sistemas, ya que éste es una forma de la aplicación del método científico a complejos problemas de los sistemas biológicos, ya que éstos existen y no han sido diseñados por el hombre, pero sí por medio de la selección natural, así que el problema es deducir la estructura del medio observado (Calow, 1976).

Cualquier abstracción o simplificación de un sistema se considera un modelo, y deberá de tener ciertos atributos funcionales importantes del sistema real, de tal modo que los experimentos con dicho modelo, puedan efectuarse con la consecuente ganancia en el conocimiento del sistema representado, su control y rápida respuesta (Fig. 1).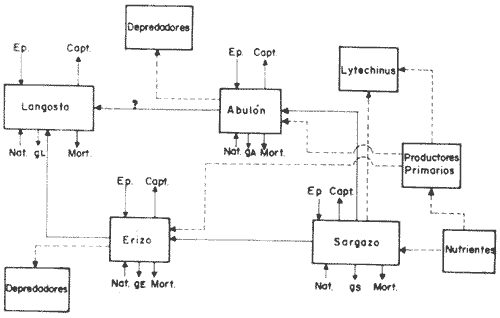

Fig. 1. Diagrama del flujo de biomasa entre las especies de la comunidad bentónica litoral, sujetas a presión de pesca, las cuales tienen las iniciales Ep (Esfuerzo pesquero) y Capt. (Captura). Con línea punteada los flujos accesorios de energía. El signo de interrogación indica el flujo de biomasa en estadios larvales, y debida a la selectividad del depredador.

Existen dos grandes tipos de modelos: los analíticos y los de simulación; sin embargo no se contraponen y ambos tratan de alcanzar en teoría, el mayor entendimiento y predicción de sistemas ecológicos y sus componentes (Dale, 1972). El alcance analítico en un modelo se refiere a una serie de procesos matemáticos para encontrar soluciones exactas. Los modelos de análisis de sensibilidad caen dentro de este grupo y determinan qué tan sensibles son sus componentes entre sí (Caswel, 1972).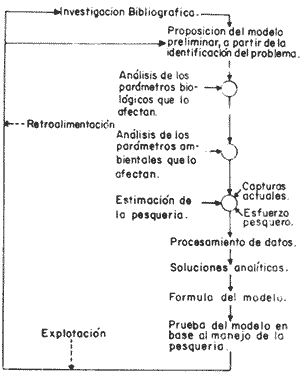

Fig.2. Programa de actividades para la formulación simulación del modelo de relaciones tróficas.

El análisis de sensibilidad determina la cantidad de cambio producido en un parámetro de un sistema dado, por el cambio en otro parámetro del mismo sistema. En este tipo de análisis existen dos tipos de sensibilidades: la sensibilidad absoluta, que representa la cantidad de cambio producida en un parámetro del sistema por unidad de cambio en otro parámetro del sistema, y la sensibilidad relativa que representa la cantidad de cambio producido en un parámetro del sistema por el cambio en otro, relativo al valor del estado estacionario de ambos parámetros (Dale, 1972), (Caswel, 1972 y Brylinsky, 1972 in Patten, 1972).

La formulación de un modelo matemático de acuerdo al análisis de sensibilidad absoluta, y que describa el flujo de energía, requiere que la entrada de energía y la pérdida de ésta en cada compartimento se exprese por medio de funciones de transferencia (Fig. 3).

Una comunidad está constituida por diferentes especies con fluctuaciones poblacionales e interacciones entre ellas y el medio ambiente. Además de la composición se necesita saber cómo contribuyen las diferentes especies a la estructura de la comunidad como un todo, qué significa la relativa importancia de las diferentes especies, y qué determina el número de especies que hacen diferente a una comunidad, "Los dos únicos enfoques posibles de una comunidad, son a nivel estructural o a nivel energético. Cuando se dá el enfoque a nivel biomasa, se entra en el aspecto ecológico o nivel energético, y los objetivos pueden ser: utilización, Optimización y planeación para no causar deterioro" (Whittaker, 1975) (Fig. 2).

Comprende el área de pesca de la Sociedad Cooperativa Libre de Producción Pesquera, Ensenada; misma que tiene como límites el Paralelo 32° 48' de Latitud Norte (Tijuana) y el Paralelo 29° 05' de Latitud Norte (a la altura de Punta Blanca, hacia el Sur).

Se realizó en la zona costera de fondo rocoso, que presenta la comunidad que vive bajo el manto de sargazo, cercana a Punta Descanso (a profundidades que van de los 7.30 metros a los 18 metros), en una de las zonas de pesca de langosta de la Cooperativa antes mencionada.

dCLa/÷dt = [(bA+bE)-(mL-nL)-gL+Σepa] (1)

dCAa÷dt = [(bSA) (mA-nA) - gA+Σepa) (2)

dCEa÷dt = [(bSE) (mE-nE) - gE+Σepa (3)

CLa = Captura de langosta en el área. (CAa ó CEa en la captura de abulón o erizo, ecuaciones (2) y (3).

ba + bE = Biomasa de erizo y abulón, ingerido por langosta.

mL - nL = Producto del número de individuos muertos menos el número de individuos nacidos; incremento de individuos langosta; lo mismo para las ecuaciones (2) y (3), con sus debidas notaciones.

gL = Gasto o pérdidas de individuos langosta como constante de estado, este gasto no está especificado, y se da al azar; lo mismo para las ecuaciones (2) y (3).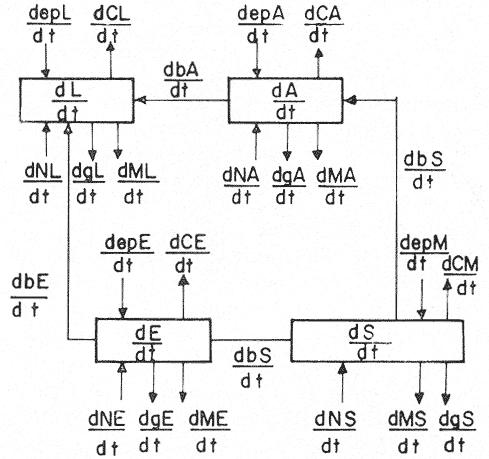

Fig. 3. Representación matemática de las variables del modelo de análisis de sensibilidad absoluta, que describe el flujo de energía por medio de ecuaciones diferenciales y funciones de transferencia.

bSA = Biomasa de sargazo que pasa a abulón (o a erizo en el caso de la ecuación 3).

Σepa = Sumatoria del esfuerzo pesquero en el área de captura. En Kg./N° de nazas/Temporada para la ecuación (1), y en "marcas", o Kg./día de trabajo/ Temporada para las ecuaciones (2) y (3).

dCAaa ÷ dt = [( bS Aa) (mAa - nAa) - gAa + Σ epaa] (2.1)

dCAna ÷ dt = [( bS An) (mAa - nAa) - gAa + Σ epaa] (2.2)

dCEfa ÷ dt = [( bS Ef) (mEf - nEf) - gEf + Σ epaf] (3.1)

dCEpa ÷ dt = [( bS Aa) (mAa - nAa) - gAa + Σ epap] (3.2)

CAaa = Captura de abulón amarilloHaliotis corrugata en el área de pesca.

CAna = Captura de abulón negroHaliotis cracherodii en el área de pesca.

CEfa = Captura de erizo rojo, Strongylocentrotus franciscanus en el área de pesca.

CEpa = Captura de erizo púrpura, Strongylocentrotus purpuratusen el área de pesca.

Los subíndices aquí añadidos, denotan las ecuaciones específicas para cada especie; estas ecuaciones provienen de las originales de captura, Ecs. (1) (2) y (3); con la salvedad de que el esfuerzo pesquero se toma por cada una de las especies.

r = Velocidad de incremento poblacional, igual a la relación (m-n), en la ecuación (4.1).

N = Número de individuos, el subíndice (a), indica la densidad de la población.

K = Denota la capacidad de carga del ecosistema, la que puede estar dada para erizo o para abulón. Iniciales E o A de las ecuaciones: (4.1) y (4.2).

dbSaA y dbSaE = Denotan la cantidad de biomasa de sargazo forrajeada por las especies de abulón y erizo en un área dada.

El resultado obtenido de la ecuación (4.2), nos va a dar un coeficiente de competencia, el cuál según el valor obtenido nos dará la información suficiente para inferir el estado de las poblaciones con respecto al mismo o mismos recursos. Hasta ahí sin entrar en profundidades mayores, porque toca esta ecuación con la teoría de sobreposición de nicho y exclusión competitiva, del área o del recurso.

Si:

α < E/A, α > A/E. Entonces sobrevive erizo.

α > E/A, α < A/E. Entonces sobrevive abulón.

α > E/A, α > A/E. Alguna especie sobrevive.

α < E/A, α < A/E. Ambas especies sobreviven.

Por sólo mencionar, se puede estudiar la sobreposición de nicho en la ecuación propuesta por Hurlbert (1978), la cual cuantifica la sobreposición en una forma más significativa:

L = (A/XY) Σ_i (XiYi/Ai) (5)

Xi = Número de individuos de la especie 1 sobre el recurso i.

Yi = Número de individuos de la especie 2 sobre el recurso i.

Ai = Es la disponibilidad del recurso i.

A = La suma de recursos disponibles.

X = La población total de la especie 1.

Y = La población total de la especie 2.

L = Índice de sobreposición de nicho.

Este cálculo y uso de la sobreposición de nichos es una de las áreas más confusas en la literatura ecológica reciente, aunque nos lleve a considerar: 1) La relación entre la sobreposición de nicho, y la intensidad de la competición, y 2) La relación entre la sobreposición de nicho y la razón de la competición inter a intraespecífica (Abrams, 1980).

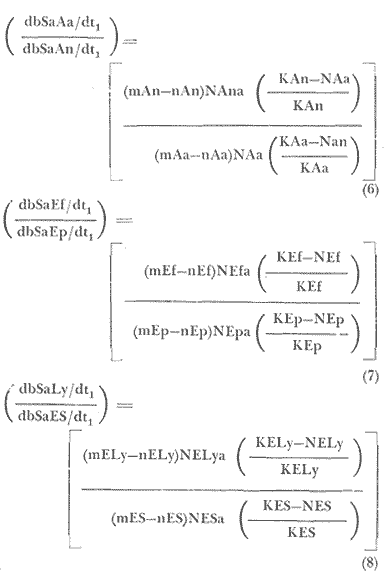En las ecuaciones (6) y (7), los subíndices denotan a la especie que compite; en la ecuación (8), se propone la competencia intraespecífica dé los géneros;Lytechinus (Ly), yStrongylocentrotus(ES).

Connel y Schroeter (1975), reportan una exclusión competitiva del erizo rojo (S. franciscanus), sobre el erizo púrpura (S. purpuratus), debido a que el primero posee espinas más largas que el segundo, por lo que puede llegar a y tocar, e irritar el epitelio de su competidor, a pesar de ser los dos igualmente abundantes, ocupan habitats similares, tienen la misma dieta y sobrepastorean aMacrocystis en zonas submareales (Dayton, 1977). Además, son especies que poseen un cielo de vida bastante rápido por lo que se desarrolló la ecuación (7) ya que además de competir por el recurso, también lo hacen por el espacio. Pero esta ecuación presenta ciertas dificultades debido a que la explotación actual, obtiene más individuos de erizo púrpura que de erizo rojo (Pineda, 1973).

Quedando, por lo tanto para la ecuación (6):

α < Aa/An, α > An/Aa. Sobrevive abulón amarillo.

α > Aa/An, α < An/Aa. Sobrevive abulón negro.

α > Aa/An, α > An/Aa. Alguna especie sobrevive.

α < Aa/An, α < An/Aa. Ambas especies sobreviven.

Quedando para la ecuación (7):

α < Ef/Ep, α > Ep/Ef. Sobrevive erizo rojo.

α > Ef/Ep, α < Ep/Ef. Sobrevive erizo púrpura.

α > Ef/Ep,α > Ep/Ef. Alguna especie sobrevive.

α < Ef/Ep, α < Ep/Ef Ambas especies sobreviven.

Y para la ecuación (8):

α < Ly/ES, α > ES/Ly. Sobrevive género Lytechinus.

α > Ly/ES, α < ES/Ly. Sobrevive géneroStrongylocentrotus.

α > Ly/ES,α > ES/Ly. Algún género sobrevive.

α < Ly/ES, α < ES/Ly. Ambos géneros sobreviven.

Hay que tomar en cuenta que la palabra sobrevivencia no implica necesariamente la muerte del competidor, sino que denota su exclusión sobre el recurso o sobre el espacio, debido a la dominancia, y está dada para un área conocida.

Para averiguar si existe asociación entre las especies, de erizo por ejemplo, sería interesante detectar la asociación por medio de una tabla de contingencia, ya que aunque existe la exclusión de una especie sobre la otra, no se sabe si constituyen una asociación ya que si el erizo rojo es removido de las bases del sargazo, el púrpura rápidamente baja a ocupar su lugar y sobrepastorea a las macroalgas y al sargazo a una velocidad mayor que la del rojo (Dayton y Connel, 1977).

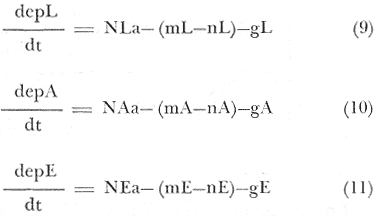En donde:

epL = Esfuerzo pesquero ejercido en el área, para langosta, dado en: Kg./N° de nazas/ Temporada de pesca.

NLa = Número de individuos langosta en el área (densidad), que se toma como el promedio de captura por unidad de esfuerzo, de cada temporada, entre el área de cada zona de pesca; quedando: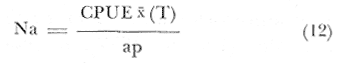

Na = Densidad relativa (Kg./Km²).

CPUEx = Promedio de la captura por unidad de esfuerzo.

T = Temporada de pesca.

ap = Área de pesca.

mL–nL = Incremento del número de individuos langosta, esta relación se da en igual forma para abulón (A), o erizo (E), de las ecuaciones (10) y (11).

gL = Gasto de individuos langosta, no especificado, y que puede estar dado por depredación o migración (lo mismo para las ecuaciones (10) y (11).

epA = Esfuerzo pesquero ejercido en el área, para la captura de abulón, dado en: Kg./día de trabajo/ Temporada. Lo mismo para la ecuación (11), referida al esfuerzo pesquero de erizo.

No se contempla la eficiencia del arte de pesca, lo que debe de tomarse como una constante de estado, en caso de emplearse su valor.

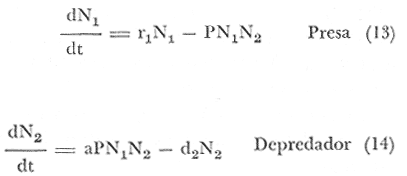r1 = Tasa intrínseca de incremento de la presa.

N1 = Densidad.

N2 = Pérdidas individuales, a una tasa proporcional a los encuentros del depredador y los individuos presa, debido al producto de la densidad de la presa y del depredador.

P = Coeficiente de depredación.

a = Coeficiente que relaciona los nacimientos del depredador a las presas consumidas.

d2 = Tasa de muerte del depredador.

Sustituyendo:

Aa = Individuos abulón por área.

Ea = Individuos erizo por área.

g = Pérdidas individuales a la tasa proporcional de los encuentros del depredador con los individuos presa. Producto de la densidad de la presa y la densidad del depredador.

N = Coeficiente que relaciona los nacimientos del depredador a las presas consumidas.

P = Coeficiente de depredación.

m2 = Tasa de muerte del depredador.

r = Tasa intrínseca de incremento de la presa.

Estas ecuaciones (15), (16) y (17), derivadas del modelo de depredación de Lotka-Volterra (citado en Whittaker, 1975) ecuaciones (14) y (13); describen las fluctuaciones cíclicas de las poblaciones de depredadores y presa. Al aumentar la densidad de población de la presa, aumenta después de cierto tiempo la densidad de la población del depredador; rebasa a la de la presa y la sobreconsume, ocasionando una baja en la población de la presa. Consecuentemente la población del depredador sigue a la de la presa, llegando a un nivel tan bajo que la población de la presa comienza a recuperarse. Esto está en la teoría, faltaría probarlo en la comunidad que estamos tratando.

Esta depredación no es dependiente de la densidad (langosta sobre abulón y erizo); lo que quiere decir que las poblaciones naturales fluctúan predominantemente en respuesta a los cambios del medio, y están controlados principalmente por la mortalidad, independientemente de la densidad.

Teniendo el medio ambiente como constante, la intensidad o amplitud de los ciclos está determinada por las densidades iniciales y prosigue siendo la misma, a pesar de la mortalidad; pueden entonces estas relaciones ser cicladas en una computadora.

La ecuación (17), involucraría a los depredadores, tales como: Panulirus interruptus, Cancer antennarius y C. Productus, Pycnopodia helianthoides, Pisaster ochrecea, Pimelometopon pulchrum, Oxyjulis californica y Scorpaenichtys marmoratus.

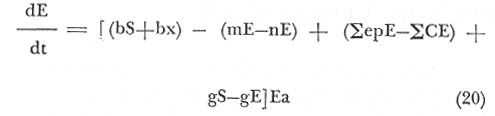A. Para Langosta: El primer término de la ecuación (18), significa los insumos por depredación de abulón, erizo y una cantidad x, constante, que entra a la población de langosta roja, y que puede ser biomasa vegetal o animal.

El segundo término, representa la tasa de incremento de individuos langosta al área de estudio.

El tercer término indica las entradas y salidas debidas al ejercicio de la pesca; como entradas, está la sumatoria del esfuerzo pesquero por temporada, y como salida, la captura de individuos langosta en la temporada de pesca.

El gasto de abulón y erizo (denotado como: gAE), representan a la porción de la población no depredada o no presente, o que por alguna razón ajena a la depredación por langosta, se pierde al alcance del modelo, por lo que se considera una constante de estado estacionario.

El gasto de langosta (gL), significa, aquellos individuos langosta depredados o ausentes por emigración u otras causas no determinadas, es también una constante de estado estacionario.

Por último el término (La), representa la densidad de individuos Langosta, estimada por un área dada y se obtiene por medio de la captura, ecuación (12), en la que se denota como Na (N = Densidad relativa Kg/Km²).

B. Para Abulón: El primer término de la ecuación (19), establece el forrajeo de abulón sobreMacrocystis, y otras especies x (Cystoseira osmundacea, Corallina officinalis var. chilensis, Eisenia arborea, Laminaria farlowii, Pterygophora californica. y Egregia laevigata), que serían los insumos de biomasa (Guzmán, Marín y Castro, 1969).

El segundo término representa la tasa de incremento de las dos diferentes especies de abulón y que son diferentes, por lo que convendría especificar con que especie se trabaja.

El tercer término referido a la pesca, es igual al de la ecuación (18), especificado para abulón.

La constante (gS), es el gasto de sargazo debido a otros depredadores que no sean el géneroHaliotis oStrongylocentrotus, pero que puede serLytechinus; o debido a la cosecha y muerte deMacrocystis, es pues una constante de estado estacionario.

La constante (gA), es igual al gasto de abulón, no determinado; es también de estado estacionario.

El término (Aa), es la densidad de población de abulón en el área, y al igual que la langosta, la obtenemos de la ecuación (12).

C. Para Erizo: El primer término se refiere al forrajeo en una forma similar a la ejercida por el abulón, ecuación (19) pero con mayor énfasis en las algas coralinas, que es en donde se encuentran gran cantidad de juveniles (Tegner y Dayton, 1976).

El segundo término, es el incremento de individuos el cual puede ser diferenciado para cada especie de erizo.

El tercer término referido a la pesca, es igual al de las ecuaciones (18) y (19), especificado para erizo.

La constante (gS) es el gasto de Macrocystisdebido a otros depredadores que no sean el géneroStrongylocentrotuso Haliotis, pero que puede serLytechinus; o debido a la cosecha y muerte, es pues una constante de estado estacionario.

La constante (gE), es igual al gasto de erizo, no determinado para la presente ecuación; es también una constante de estado estacionario.

El término (Ea), que multiplica a la ecuación, es la densidad de población de las diferentes especies de erizo en el área, y al igual que las ecuaciones anteriores (18) y (19); se deriva de la ecuación (12).

Este coeficiente o función de transferencia, es una constante de velocidad con unidades de tiempo¹ y representa el número de veces que una cantidad de energía igual al flujo de energía en cuestión, va a fluir a través del compartimiento en la unidad de tiempo. (Patten, 1972).

Es conveniente considerar dentro del modelo de transferencias, una ecuación particular sobre sargazo, la cual quedaría como sigue: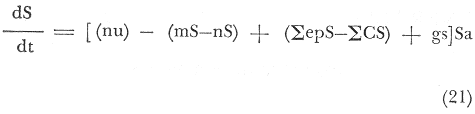

El primer término, denotaría la disponibilidad de nutrientes (nu), y el aprovechamiento de estos.

El segundo término, denotaría la tasa de incremento de la población o manto deMacrocystis.

El tercer término, sería el esfuerzo de recolecta o corte-extracción de sargazo, expresado en las siguientes ecuaciones: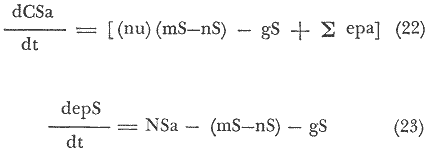

La ecuación (22), nos dá, el corte del manto de sargazo.

La ecuación (23), denota el esfuerzo pesquero, dado también en "mareas", o Kg./día de trabajo/ Temporada. Aquí existe un problema de normalización del esfuerzo, ya que mientras, los buzos recolectan el sargazo (Macrocystis pyrifera) y Gelidium (Gelidium robustus), el barco Sargacero, sólo corta la cúpula del manto; cuya normalización dependería del esfuerzo de pesca, dado para el presente trabajo en Kg./día de trabajo/Área.

El cuarto término (gS), estaría dado por el gasto de sargazo debido a la depredación por los génerosHaliotis,Strongylocentrotus yLytechinus como principales consumidores, y también debido a pérdidas por condiciones fuera de control, como oleaje extremo, etcétera.

El término (Sa), sería la densidad de la población del manto o "standing crop" de la cúpula del manto que está sujeta a corte.

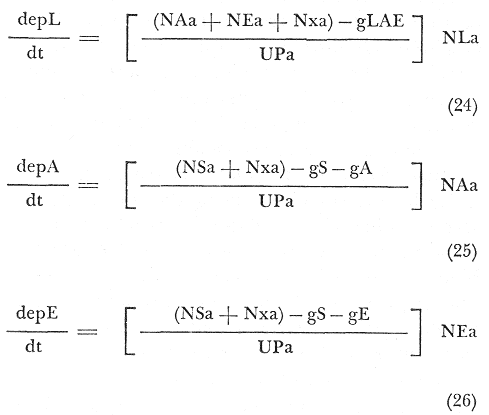depL = Esfuerzo pesquero aplicado a langosta.

NAa + NEa = Densidad de abulón y erizo.

Nxa = Densidad de x fuente de biomasa en el área.

gLAE = Gasto no especificado de langosta, abulón y erizo.

NLa = Densidad de langosta en el área.

depA = Esfuerzo pesquero aplicado a abulón.

depE Esfuerzo pesquero aplicado a erizo.

gA = Gasto no especificado de abulón.

gE = Gasto no especificado de erizo.

gS = Gasto no especificado de sargazo.

UPa = Número de unidades de pesca en el área.

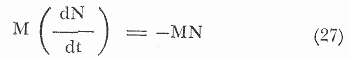Esta forma se utiliza para inferir que la mortalidad se debe a un sinúmero de causas que actúan al azar, y que la probabilidad de un individuo en particular, de morir entre el tiempo T y T+T, es constante.

Es de suponer que la mortalidad natural, varía con la densidad de la población, se asume que la ecuación (17) puede representar la tasa de mortalidad natural, siendo el coeficiente m², constante y efectivo a partir de la edad de reclutamiento.

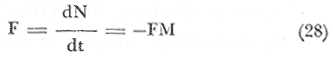Teniéndose entonces, que el coeficiente de mortalidad por pesca F, es directamente proporcional al esfuerzo pesquero (ep), lo que se expresa en la siguiente relación.

F = Cep (29)

Donde C, es una constante que representa la capturabilidad de los individuos.

A efecto de una buena respuesta del modelo, sería conveniente estandarizar el esfuerzo pesquero, ya que en la pesquería de langosta, el número de nazas que se utiliza por unidad de pesca varía, según las condiciones en que se encuentren estas en el momento de la pesca; además, ocurre también, que dependiendo de la fuerza de la corriente, algunas trampas se estropean durante la temporada de pesca, variando así el número de nazas por área (las que nunca tienen un número igual de nazas por área). Por lo que es necesario introducir una variable de gasto para esfuerzo pesquero, la que sería una constante de estado estacionario, y no solamente para la ecuación de langosta, sino para abulón y erizo también.

En las especies de abulón y erizo, la variabilidad es aún mayor que en el caso de langosta, ya que por ser la pesquería manual ("mareas" o Kgs/día de trabajo), la diferencia se presenta en la habilidad de cada uno de los buzos y el lugar donde opera.

Panulirus interruptus, es una especie migratoria, que se acerca a la costa anualmente para reproducirse de marzo a agosto, a diferencia deHaliotis spp y Strongylocentrotus spp, los que siempre están presentes. Por lo que sería conveniente añadir un factor limitativo de tiempo en las ecuaciones de depredación, o cambiando el depredador principal estacionalmente.

Existe información contradictoria con respecto a la relación trófica de la langosta hacia el género Haliotis por lo que su modelo se desarrolló indistintamente de el géneroStrongylocentrotus, a lo largo del estudio, ya que con la ecuación de competencia y la tasa intrínseca de crecimiento de la población, se puede llegar a situaciones más apegadas a la realidad.

En lo que respecta a la predicción, es de desearse la obtención de datos reales para adecuarlos al modelo, así como los datos de factores ambientales, pues las predicciones de éste modelo son determinísticas; es decir, los factores ambientales que afectan a cada compartimiento están en equilibrio, son constantes e independientes de la densidad de población, y, que no hay migración; cosa que en un sistema real no sucede, pues estos factores están controlados estacionalmente y se pueden dar al azar, al tiempo que sus magnitudes son impredescibles.

En lo que respecta a los factores bióticos (simulación), como la competencia, se presentan situaciones más difíciles de medir realístamente, por lo que es de esperar que ésta simulación esté aún más alejada de la realidad (Fig. 4).

En cuanto a la simulación de los aspectos pesqueros, ésta va a depender directamente de la periodicidad de las temporadas pasadas, comportándose cíclicamente lo que nos permitiría definir periodos de mayor o menor productividad anuales debidos a la situación real del recurso (a su densidad) y reflejado en la pesquería, entonces, sí se puede hacer una simulación de la tendencia de la pesquería en la zona.

La ecuación (1) de langosta y las ecuaciones (2) y (3) de abulón y erizo respectivamente; están obligadas a funcionar con entradas de biomasa seleccionada, debido a que proporcionándole entradas x (otras fuentes de alimentación), no se puede simular con el modelo como tal para obtener respuestas de índole pesquera, ya que de la otra forma, estaría ecológicamente obviado.

Las ecuaciones anteriores están tratadas por especie, para poder darles valores estimados o derivados de los datos de captura y establecer un juego de entradas y salidas, para así obtener determinadas situaciones y posibles respuestas para el adecuado manejo.

En cuanto a competencia, y de acuerdo a los ciclos individuales de las especies de erizo del géneroStrongylocentrotus, aunque están reportadas iguales; con datos sobre el reclutamiento se pueden aventurar situaciones como la presentada en la figura 5, donde se nota el desfasamiento causado por la sobreexplotación de una de las especies S. franciscanus, y su posible efecto en el reclutamiento de nuevos individuos, lo que necesariamente nos reduciría las poblaciones de erizo y de abulón, ya que ambos utilizan la cúpula de espinas de S. franciscanus en los estadios juveniles como protección (Tegner y Dayton, 1976).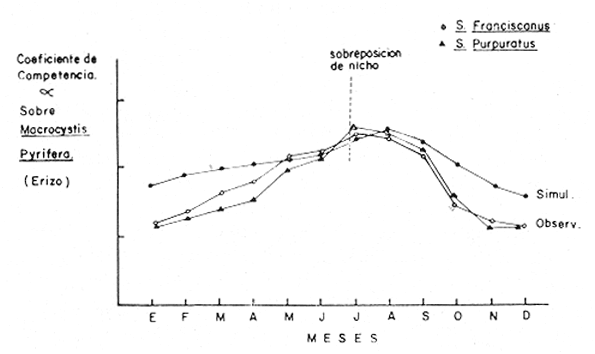

Fig.4. Relación de la simulación de la competencia y los valores de los coeficientes de competencia (α) observados. Se entra en aspectos más específicos, como el de la cuantificación de la sobreposición de Nicho, lo que no es factible de hacer en simulación sin alejarse de la realidad.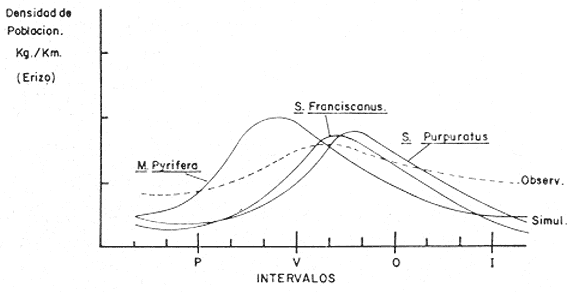

Fig. 5. Desfasamiento del reclutamiento de Strongylocentrotus franciscanus, causado por la sobreexplotación (Tegner y Dayton, 1976), lo que causaría un "retraso" en el reclutamiento de nuevos individuos, no sólo del género Strongylocentrotus spp, sino también del género Haliotis spp. (Idem).

Por lo expresado anteriormente, convendría hacer modificaciones al modelo, introduciendo variables de talla mínima en las ecuaciones de transferencia, o hacer un tratamiento de clases de edad, obtenido de los datos biométricos de los individuos pescados, para detectar sobre qué clase de edad se está incidiendo más, y cómo afecta esta extracción a la comunidad.

Como la langostaPanulirus interruptus, y el cangrejoCancer spp, presentan grandes desplazamientos nocturnos en busca de alimentación, mientras que en el día se encuevan para protegerse, por lo que es necesario hacer énfasis en que la ecuación de depredación tenga factores de tiempo más estrictos (Diurno-Nocturno).

Se excluyó al sargazo candeleroPelagophycus porra, el que aunque importante por sostener una comunidad similar, no es de tan fácil observación por encontrarse a profundidades que van de los 20 a los 40 metros.

Este modelo no es una representación realista de la comunidad natural de la cual fue derivado, pues tiene lógicamente deficiencias en la cuantificación de las entradas (o relaciones) biológicas. Ya que la forma en que los compartimentos están matemáticamente relacionados es también poco real.

El modelo propuesto para depredación, es independiente de la densidad y por lo tanto no es un modelo determinista, pero, como Whittaker (1975) hace notar, "ésta depredación independiente de la densidad es uno de los principales controles del medio ambiente en la comunidad".

La estabilidad de la comunidad es afectada por la extracción de sus diferentes componentes; en base a explotaciones muy estructuradas, y no se pueden más que referir los cambios que en ella sucedan a una relación Captura/Corte en el tiempo, ya que éste es determinante de la extracción de individuos de las especies mencionadas.

Esta Captura/Corte/Tiempo, está relacionada directamente con la abundancia relativa de las especies y su densidad, ya que a un mayor tiempo de explotación, más afectada estará la población, pudiendo llegarse a su sobreexplotación (sobre todoMacrocystis), debida al incremento del Esfuerzo Pesquero o las Unidades de Pesca, los que influyen selectivamente en las relaciones interespecíficas de la comunidad. Lo mismo que sucedería entre especies que compiten llegando ala exclusión; o especies que son devoradas por otras pudiendo llegar a la extinción. Obviamente es más sencillo que ocurra lo primero, ya que la acción de pescar, es una acción pensada e instrumentada y muchas veces no controlada; aunque es dependiente de la densidad de población que está sujeta a la presión de pesca.

Los autores agradecen a T. Brand sus valiosos consejos; asimismo agradecen también a A. Farías, su ayuda en lo referente a la investigación bibliográfica.

Aviso de Privacidad

Cerrar esta ventana